I.2.7
2/8/2021

HI. Since this is supposed to be a daily thing. I finally wrote a messy bash script (using this sample file) to help me generate these posts. Pls no laff. "L0l0l0l You fucking n00b. Instead of 'basename $PWD' you should be using '${PWD##*/}' in order to avoid creating a subprocess and save 0.0000000000001 precious seconds." Yeah, yeah, whatever, fucko. And yes, because the make4ht output has line breaks at very awkward spots, I used some pretty nasty sed commands. I had to learn about BRANCHING, YO.
ANYWAY, let's start the exercise. For part (a), just use yesterday's mess:
| n + 1 | = dim S(Pn) | ||
| = dim Pn + 1 |
That was easy. Hey, the hint says to use yesterday's mess for part (b) too!
1.10 is this guy:
 (So, it turns out this is another "projectivization of affine" thing)
(So, it turns out this is another "projectivization of affine" thing)So how do we hook up 2.6 and 1.10?
Well, Y being a quasi-projective variety means its an open subset of some projective variety. Actually, by 1.6, Y is precisely that variety (or at least the smallest such variety). Now, the bar notation for closure is going to be a little too ambiguous in this exercise, so let's move everything to the cl notation, and we'll be using this property a lot:
"If A is a subspace of X containing S, then the closure of S computed in A is equal to the intersection of A and the closure of S computed in X: clAS = A ∩ clXS"
I.e. Let's call X = Y , so we can instead write X = clPnY . And note that clX(Y ) = clPn(Y ) ∩X = X ∩X = X.
. (So our goal in the new notation is to show dim X = dim Y )
Okay. Now let's use the homeomorphism from last time ϕ : X ∩ U0 → Y 0. We saw last time that
 | (1) |
So what happens to the closure of Y when intersected with U0? Well:
| clX∩U0(Y ∩ U0) | = clX(Y ∩ U0) ∩ (X ∩ U0) | |||||
| = X ∩ X ∩ U0 | 1.6 again: since Y and U0 are both open in X | |||||
| = X ∩ U0 |
And since ϕ is a homeomorphism, closures commute:
| clY 0(ϕ(Y ∩ U0)) | = ϕ(clX∩U0(Y ∩ U0)) | ||
| = ϕ(X ∩ U0) | |||
| = Y 0 |
I.e. in "bar" notation:
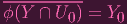 | (2) |
And hence, by 1.10:
| dim Y 0 | = dim ϕ(Y ∩ U0) | |||||
| = dim Y ∩ U0 | (ϕ is a homeomorphism) |
 | (3) |
Holy shit this is getting messy. Let's just apply exercise 1.10a to finish it off.
| dim X | = dim Y ∩ U0 | |||||
| ≤ dim Y | 1.10a |
(ACTUALLY, I just realized I could have just used 1.6 again to say dim Y = dim Y ∩ U0. WHATEVS)
Oh, and since I just realized that neocities allows you to upload txt files, I guess I might as well start linking the corresponding tex files for each post. Here's today's one. ALSO, yes, I need to figure out how to not make the equation descriptions jut out of my post. fffuuuuuuuggggg.