I.2.6
2/6/2021

This exercise is sort of another projectivization of an affine result:

HOWEVER, note that we have dim S(Y ) = dim Y + 1 instead of dim S(Y ) = dim Y , so things are different
from affine land. As you can tell from reading the hint, this is going to be more complicated to prove than prop
1.7.
First of all, why doesn't the prop 1.7 proof work here? Well, 2.4(a) and (b) tells us that there is a correspondence
between irreducible sets and prime HOMOGENOUS ideals. When we consider a chain of primes in S(Y ), they do
not correspond exactly to a chain of irreducible algebraic sets in Y , because there might be some
nonhomogenous primes mixed in there. So that's why we have to do the fancy shmancy stuff the hint tells us to
do.
Okay, let's begin. The hint refers to (1.7) (which is above), and (1.8A):
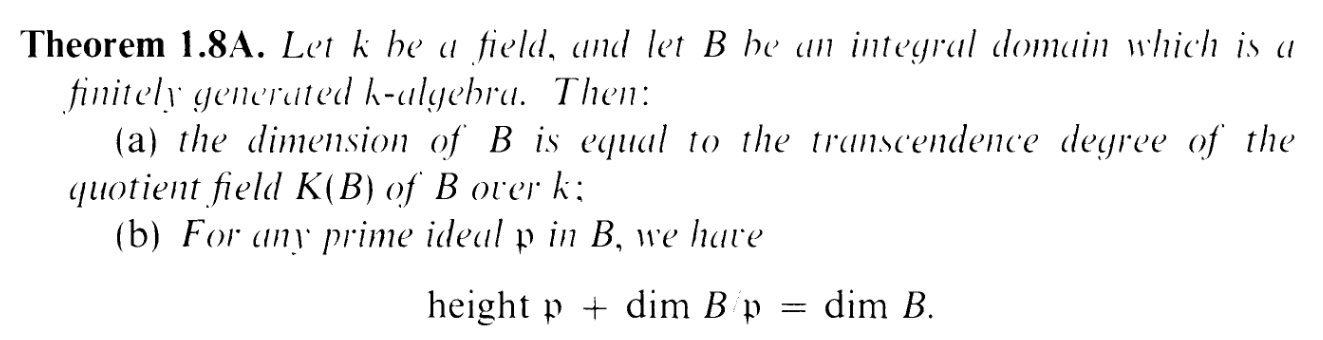
It also refers to (Ex 1.10), and we'll just be using part (b):
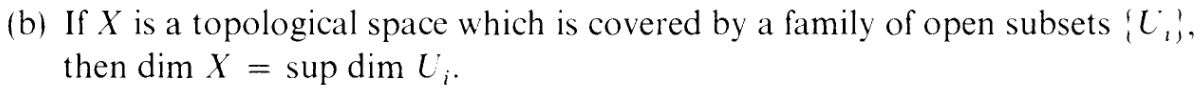
The ϕi the hint is referring to is this guy:

Oh goodness. Another exercise where we have to convert between affine and projective. And this time in a
DIFFERENT WAY from what we had to do in (2.1).
Okay, so here's the overall strategy. Using the corollary to (2.2):
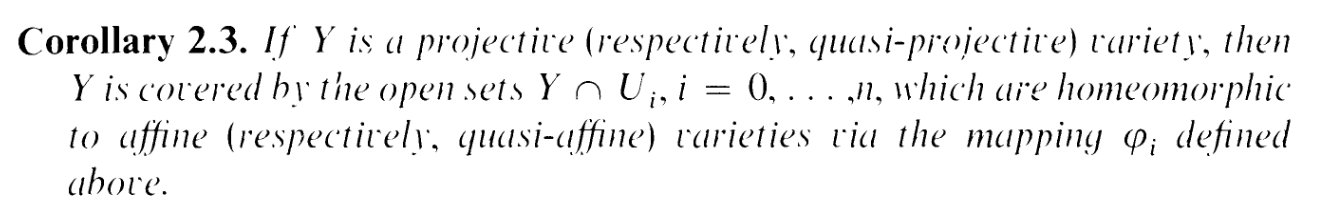
we establish that the Y ∩ U0,…,Y ∩ Un make a (finite) open cover. Assume without loss of generality that
sup Y ∩ Ui = Y ∩ U0. (EDIT: Actually, they're all homeomorphic, so they all have the same dimension lol). Now check this out. *AHEM*
| dim Y | = sup dim Y ∩ Ui | By 1.10(d) | ||||
| = dim Y ∩ U0 | By assumption | |||||
| = dim Y 0 | Y ∩ U0 and Y 0 are homeomorphic by ϕ | |||||
| = dim A(Y 0) | by Prop 1.7 |
I.e. we have:
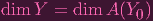 | (1) |
Did you like that string of equalities? Heh, don't worry, we have more on the way (save me).
Now, by definition, A(Y 0) = k[x1,…,xn]∕P for some P. Ready for the next string of equalities? YE BE
WARNED: It's going to be more tenuous than the first string. More tenacious:
i.e.
![dim A (Y0)[x0,x- 1] = dim A (Y0) + 1
0](Ip2p61x.png) | (8) |
Also, take for granted that we can get to
![- 1
S (Y)x0 = A(Y0)[x0,x 0 ]](Ip2p62x.png) | (9) |
At the least if you get to the part at the hint where it identifies A(Y 0) = (S(Y )x0)0 (The right hand side refers
to the zero degree elements of S(Y )x0 then the equality is pretty easy to see. "What about the part up to that
identification?" It's a gigantic pain in the ass and I don't think it's worth it. Trust me. Just take that for granted.
"Umm, bro, you're asking me to make a lot of leaps of faith right now." Ain't that life? Leap, my friend! Leap into
my chest!

Okay, so if you combine (1), (8), (9), you get
 | (10) |
"Wait, that doesn't seem right. We wanted S(Y ) = dim Y + 1. What's with that x0?" Good question, reader. If
we want this all to work out, we'd better have:
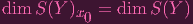 | (11) |
"But, does that make sense? What's the intuition behind that equality?" HAH, FUCK INTUITION. I SPENT A
GOOD AMOUNT OF SECTION 1 TRYING TO PICTURE ALL THOSE AFFINE SURFACES AND
CONCEPTS, BUT I DON'T HAVE A FUCKING CLUE WHAT'S GOING ON PICTORIALLY IN THE
PROJECTIVE CASE. I'M JUST MANIPULATING EQUATIONS. I'M. JUST. FUCKING. AROUND. WITH.
SYMBOLS. I DON'T KNOW WHAT'S GOING ON. FUUUUUUUUUUUUUUUUUUUUUUUUUCK.
This is where I got stuck for a good amount of time. ARE YOU READY, LADIES AND GENTLEMEN? IT'S THE
HOLEINMYHEART ADMIN'S FUCKUP CATALOGUING TIME. I know, I know, it's been a while. The
exercises have gone too smoothly lately. You were starving for details of my shitty tangents. Well, here we
go:
I first looked up "Krull dimension of localization" and stumbled into Wikipedia saying, "the height of 𝔭 is the Krull
dimension of the localization of R at 𝔭." I proceeded to attempt to calculate the height of the ideal (x0), supposed
that it was 1, only to realize that I would be proving that dim Y = 0. Well, that's obviously not right, lol. Of
course, I realized the localization at (x0) is different from the localization at "x0", and (x0) might not even be
prime in S(Y ) in the first place, so that statement isn't very helpful. I wasted about an hour on
this.
What else did I try? Well, after some googling, I was reminded of the bijection between the prime ideals of S(Y )x0
and the prime ideals of S(Y ) that don't contain x0. Ah, so right off the bad we have dim S(Y )x0 ≤ dim S(Y )
(since the latter has more prime ideals). If I just show the reverse equality, I'll be solid. Fuck yeah. I wasted 2 hours
fumbling around getting nowhere.
WELL THEN. Perhaps the equality isn't true at all? Perhaps something went wrong in that tenuous string of
equalities. Perhaps I actually have to think about transcendence degrees beyond just adding +1 where it's vaguely
convenient. SHIT, SHIT, SHIT. I DON'T want to work with transcendence degrees, man. I have to think about...
algebraically independent subsets? Ugh. UGH.
Well, turns out the solution does have to do with transcendence degrees, but I don't have to go in and
iron out my magical +1. In fact, erm... You can just use 1.8A again, and use the obvious fact that
K(S(Y )x0) = K(S(Y )):
| dim S(Y )x0 | = trdegK(S(Y )x0) | By 1.8A(a) again... Well, you have to show that S(Y )x0 is an integral domain. "Let me guess. Take it for granted?" Hell yes, motherfucker. | ||||
| = trdegK(S(Y )) | ||||||
| = dim S(Y ) | 1.8A(a) |
I was worried about this mess: trdegK((k[x1,…,xn]∕P)[x0]) = trdegK((k[x1,…,xn]∕P) + 1... with good reason. But if you just think of this as trdegK(R[x0]) = trdegK(R) + 1 then it's pretty easy to see it, I think. Adding an indeterminate into the field is just a free extra element you can add to the transcendence basis of R.
Also I was wondering if S(Y )x0 is an integral domain. It is. In fact ANY localization of an integral domain is an integral domain. I proved this very quickly in my notes.
ALSO, the dreaded A(Y 0) = (S(Y )x0)0, which is the heart of the projective-affine conversion nitty gritty shit for this exercise, is doable. I sketched out the proof in my notes.
I may edit this post or make a separate post later to fill these in, but it's getting late. Soz for the omissions. "Omit yourself". OOOOOHHHHHHHH!