Another easy one. Let's go:

(a):

I'll set:
A = {Algebraic sets in Pⁿ} and
B = {homogenous radical ideals in S}-{S₊}
And let's restrict Z(⋅) and I(⋅) to these domains correspondingly:
Z : A → B by Y I(Y ) and
I : B → A by αZ(α)

Then given α ∈ B, we have I(Z(α)) = according to 2.3(d). "BUT WAIT, MR. HEARTLESS FAGGOT." Idiot. I have a heart, it's just divoted (I'm not empty, just evil). And as for the "faggot" part... errr... just continue. "B excludes the so-called 'irrelevant ideal' S₊, BUT IT DOESN'T EXCLUDE S, DOES IT? S is certainly homogenous, since S = (1), so it's actually RELEVANT. But to apply the equality you just did, 2.3(d) assumes that Z(α)≠∅, And this isn't true for α = S." Well, Mr. Strawfaggot, reread what I said in that post. That's right. I lubed this post up with a careful demarcation. Indeed, the equality works for α = (1), and thus we're SAFE.


Anyway, = α by definition of B, so we actually have I(Z(α)) = α, so I is a left inverse of Z.

Now, given Y ∈ A, we have Z(I(Y )) = Y . And Y = Y since Y ∈ A is algebraic i.e. closed. So I is a right inverse of Z. Hence Z^-1 = I (when restricted to these domains of course). And the inclusion reversing comes from 2.3(a) and 2.3(b).
So (a) is DONE.

By the way, like the first 3 exercises, part (a) and (b) is just a projectivisation of an affine proposition:

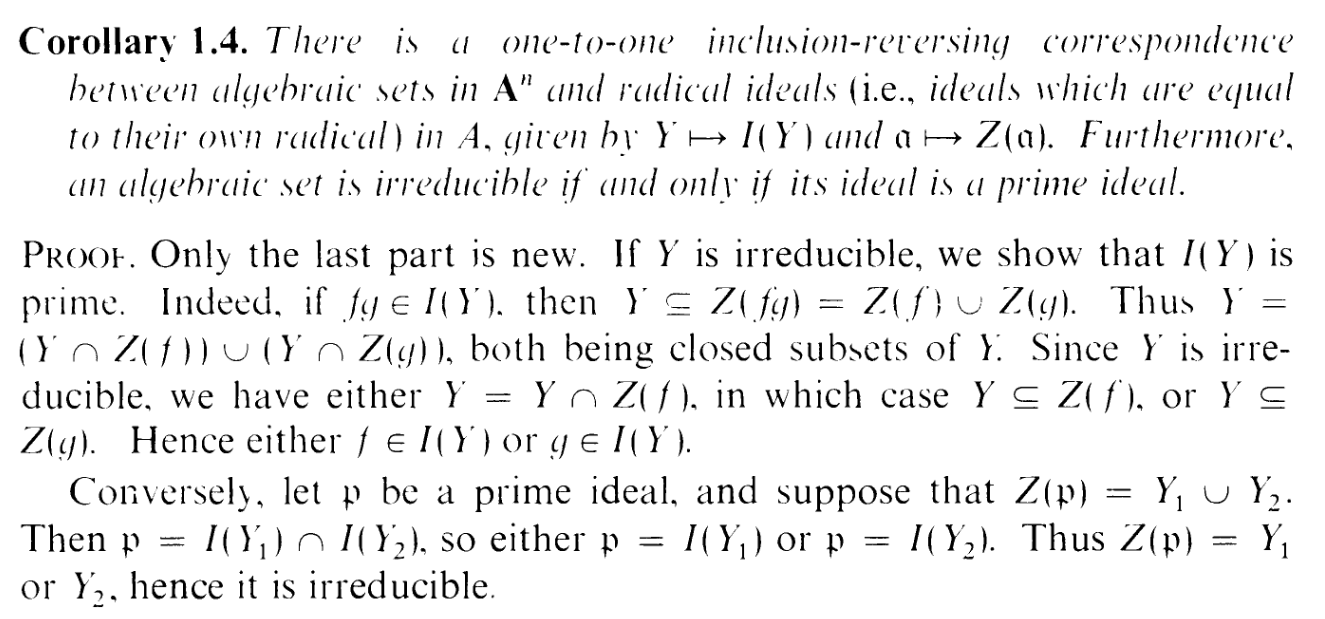
I did go through the trouble of doing part (a) to handle the new α = (1) exception. But the proof of (b) is identical to the one for the affine case, so there's no work do do here.

And what about part (c)? Well...

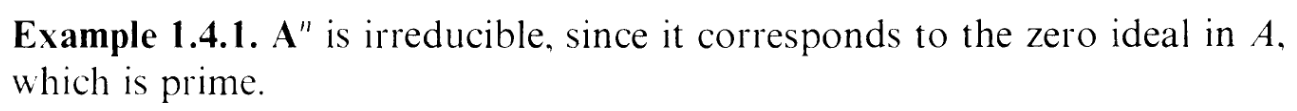
Yeah. Aⁿ and Pⁿ share the same coordinate ring (essentially; just an x₀ off), so the same argument works here.

So we're done.
I'm BLAZING through these exercises baby (More like they're babby mundane exercises and I'm going to get fucked in the butthole by 2.6).