I.2.12d
2/24/2021

I run GNOME 3, currently. I am not very picky on desktop environments. GNOME 3 is fine for me, for the most
part. I used to run XFCE, which was also fine. I don't have a strong preference. But when I first used GNOME 3,
there was an issue. There was this "feature" called a "hot corner". Whenever your mouse touches the top-left of the
screen, even if you don't click anything, it automatically brings up an "activities overview" that you have to exit out
of.
This feature, pissed me off. Every time my mouse scraped the top left corner of the screen, the DE decided, "OH,
THIS SEEMS LIKE A GOOD TIME TO FUCKING HOG THE USER'S SCREEN". Imagine having a fucking
"feature" that OPENS UP A NEW INTERFACE WITHOUT THE USER CLICKING OR PRESSING
ANYTHING. AND IT'S THE DEFAULT SETTING. No, NO. It's WORSE than default. Want to disable it in the
settings? Nowhere to be found. What you have to do is install gnome-tweak-tool, and then ON TOP OF
THAT, you have to install a third party extension to disable it. Oh, actually, GNOME 3.34, released in
September 12 2019 (Yes, like a sequel to 9/11. Coincidence?) added an option to disable it. Ah, thank you
devs, for listening to the users and promptly fixing that issue... until you look at the comment history
on that extension page and realize that that hte issue goes back NINE FUCKING YEARS (not to
mention people mentioning they still need the extension because the in-house disabling isn't working
correctly).
Like I said, I'm not picky about UI and aesthetics. And I'm not a technical guy either. Back when I was even
less proactive about tweaking out inconveniences in my system, I let this "hot corner" sit for several
months. After all, there was no option to disable it in the settings, and the default fix was for a version
more recent than mine (ahh, Debian stability). So I dealt with it. And dealt with it. I don't know how
tech nerds think, but think about it from a non tech nerd perspective: What prompts a user to fix an
inconvenience? You see, at first, the inconvenience is just an inconvenience. It's just slightly annoying. The user
can deal with that. Then as the inconvenience keeps erupting, the user gets annoyed enough to look
for a way to disable it. They can't find it in the "Settings" area, and they have 10 tabs of trap porn
open that they need to take care of, so they decide to leave it alone and just deal with it. Then the
inconvenience starts to discombobulate the user while they're trying to do basic shit. You're in the
middle of typing out a line of dialogue for the VN script you're working on (just fucking admit it
you have one too), your elbow hits your mouse, and the mouse bops the top-left corner and just as
you're typing the word "recalcitrant" the FUCKING ACTIVITIES CORNER TAKES OVER YOUR
SCREEN. Then it happens again, and again, and again, and you start to get homicidal thoughts.
You start fantasizing about strangling the person who was responsible for this shitty feature. Yes, the
dev who added this feature probably knows 99999 times more about UI and programming than me,
and is probably an actually good, dependent person, with a family and kids, or maybe even just a
significant other to whom he can be there for, whereas I've accomplished nothing in my life and haven't
helped anyone with anything ever BUT I STILL WANT TO STRANGLE THIS COCKSUCKING
ASSLICKING SHITFUCKING WORTHLESS FUFCKFACE FOR ADDING THIS FUCKING WORHTLESS
FUCKING "HOT CORNER" FEATURE THAT IS COMPLETELY FUCKING IDIOTIC. Basically, the
typical user isn't proactive: They have to reach a boiling point: They have to reach a point where
they realize they're irrationally wishing for the death of someone that has done nothing bad towards
them.
Now, those thoughts are extremely irrational. To hate a person you've never met, have no context about, other than
the fact that they added in a single inconvenient feature to a program. It's a very abstract, irrational sort of hatred,
indeed. But there is some flesh to it. At least it is directed towards a hypothetical living human being. "I want to
strangle the person that is responsible for this feature". And that kind of thought, albeit irrational, is actually quite
common, especially on the internet. It's not crazy, it's just a sign that you actually need to get your shit together
and fix something.
However: Let me ask you this. Have you ever wanted to strangle a twisted cubic curve? I have. On this fine night.
Yes. I've reached this level of abstract hatred. I had enough trouble with it back in 2.9b, but with
this exercise, I've fucking had it with this fucking curve. Yes, I FUCKING HATE THE TWISTED CUBIC CURVE.
But don't worry, clearly the feeling is mutual. It hates me. It wants me to fucking lose. Why is it that everytime
that I come across it, the mathematics around it turn into some crazy voodoo fuckery? I don't fucking get this exercise
at all. And yes, I'm being sincere: While trying to do this exercise, I actually had the urge to strangle the twisted
cubic curve. I actually felt that towards a mathematical object. Although, of course, the situation is the reverse: it's the twisted cubic curve that's strangling
me.
Let me show you why I'm complaining so much. Last time, back in 2.9b, the exercise required me to pull out a
certain F1 polynomial out of thin air. What does this exercise have in store for us? Fucking absurdity, that's
what.
The Wikipedia page already gives us the mapping for ρ:
 |
Which means we can write the corresponding θ as:
| θ : k[x,y,z,q] | → k[s,t] | ||
| x |
 s3 s3 | ||
| y |
 s2t s2t | ||
| z |
 st2 st2 | ||
| w |
 t3 t3 |
And what we showed in 2.8 was that the twisted cubic curve is the variety C = Z(β) where β = (F0,F1,F2), where
| F0 | = xz - y2 | ||
| F1 | = yw - z2 | ||
| F2 | = xw - yz |
So our goal is to show that imρ = Z(β). Now we actually know from (b) that imρ = Z(α) (where α = ker θ), so if we show that α = β, that will be sufficient.
The invlusion β ⊂ α is pretty obvious, so the main challenge is showing α
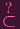 β. Okay. Give me some g ∈ α.
To show that g ∈ β, I need to show that it is generated by F0,F1,F2. What's one tactic we've
used over and over on this blog to do this sort of thing? That's right! Euclidean division Let's give
it a shot: If you interpret g as an element of k[y,z,w][x], then when you divide by F0, you get
β. Okay. Give me some g ∈ α.
To show that g ∈ β, I need to show that it is generated by F0,F1,F2. What's one tactic we've
used over and over on this blog to do this sort of thing? That's right! Euclidean division Let's give
it a shot: If you interpret g as an element of k[y,z,w][x], then when you divide by F0, you get
| g | = F0q0 + r0 |
where r0 ∈ k[y,z,w] (since F0 had degree 1 in x)
Then thinking of r0 as an element of k[y,z][w], let's divide it by F1. This gives us
| g | = F0q0 + F1q1 + r1 | (1) |
And r1 ∈ k[y,z]
Problem: we can't just go ahead and divide by F2 = xw - yz now, because this element has both x and z in it, and thus isn't an element of k[y,z] but k[x,y,z,w]! If we divided by it, we'd be reintroducing the x and z, undoing the work we did to get rid of it.
So maybe I didn't pick the most optimal order/choices in my division steps. But try it yourself, reader. Maybe start with F2 this time, taking out the z. And then follow up with F1, taking out the y. Oof, then F0 reintroduces both variables. I'm pretty sure there's no combination that works. So are we screwed?
Well, let's just go along and apply θ on (1) and see what happens. Since g ∈ ker θ, as do F0 and F1, we get
| 0 | = θ(r1) |
Okay, now here's the thing. r1 is an element of k[y,z] that maps to 0 under θ. Can you think of any nonzero element that would do that? I can't. I actually think that r1 has to be 0. If you're unconvinced, let me explain. Let's use the multinomial notation for r1 and collect like terms, so we can write
| r1 | = ∑ iγiXδi |
where γi ∈ k, each δi = [ai,bi] is distinct (since we collected like terms)m and so Xδi = yaizbi. Now we know that this becomes 0 when we map it under θ, so more specifically, we can write
| 0 | = θ(∑ iγiXδi) | ||
| = ∑ iγiθ(yaizbi) | |||
| = ∑ iγiθ(y)aiθ(z)bi) | |||
| = ∑ iγi(s2t)ai(st2)bi) | |||
| = ∑ iγis2aitaisbit2bi | |||
| = ∑ iγis2ai+bit2bi+ai | |||
So the exponent vectors for the new polynomial are ϕi = [2ai + bi, 2bi + ai] (running out of greek letters lmao). Now, is there anyway that two of these exponent vectors can be equal? Say we had ϕ1 = [2a + b, 2b + a] and ϕ2 = [2c + d, 2d + c]. Then for them to be equal, we'd need to satisfy:
| 2a + b | = 2c + d | ||
| 2b + a | = 2d + c | ||
i.e.
| 2a + b - 2c - d | = 0 | ||
| a + 2b - c - 2d | = 0 | ||
Yep. Welcome back to linear algebra folks! Stick this into an augmented matrix and we get
![[2 1 - 1 - 1 0]
1 2 - 1 - 2 0](Ip2p12d6x.png) |
And
![[ ]
1 0 - 1 0 0
0 1 0 - 1 0](Ip2p12d7x.png) |
i.e.
| a | = c | ||
| b | = d | ||
Which means that their preimages came from a single exponent vector: δ = [a = c,b = d], i.e. they came from like terms Y aZb and Y cZd which is a contradiction: the ϕs can't be separate because we already collected the like terms, so they would have been collected together in the summation after θing it. Hence, each ϕi is a distinct exponent vector. Which means that in order for the polynomial to be 0, we need γi = 0 for all i. But then this means that r1 itself is 0. So we can write (1) as
| g | = F0q0 + F1q1 | (2) |
Oh, nice, so g is generated by just the first two polynomials, which allows us to conclude g ∈ β, like we needed. Done.
Wait..... just the first two polynomials?. JUST THE FIRST TWO POLYNOMIALS? I just showed that α ⊂ β, even if I just let β = (F0,F1). And this doesn't ruin the β ⊂ α inclusion either (in fact it makes it easier!). So... WHAT THE FUCK HAPPENED TO F2????? I THOUGHT I NEEDED ALL OF F0,F1,F2 TO GENERATE THE IDEAL FOR THE TWISTED CUBIC CURVE, BUT I ONLY NEED F0,F1????? BUT THAT MAKES NO SENSE. THE WIKIPEDIA PAGE SAYS THAT YOU NEED ALL THREE. Ah, maybe Z(F0,F1) = C, but I(Z(F0,F1)) =
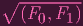 , and we need to add in the F2 in order to get rid of the radical?
NOPE. Remember α is prime. I just "showed" that α = (F0,F1), so then we'd actually have that
, and we need to add in the F2 in order to get rid of the radical?
NOPE. Remember α is prime. I just "showed" that α = (F0,F1), so then we'd actually have that
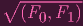 = (F0,F1), therefore I(C) = (F0,F1).... BUT THIS CAN'T BE THE FUCKING CASE AT ALL,
UNLESS THE F2 IS EXTRANEOUS WHICH I'M GUESSING IT'S NOT SINCE IT WAS INCLUDED
BOTH ON THE WIKIPEDIA PAGE AND IN 2.8. SO WHAT THE FLYING FUCK IS GOING
ON.
= (F0,F1), therefore I(C) = (F0,F1).... BUT THIS CAN'T BE THE FUCKING CASE AT ALL,
UNLESS THE F2 IS EXTRANEOUS WHICH I'M GUESSING IT'S NOT SINCE IT WAS INCLUDED
BOTH ON THE WIKIPEDIA PAGE AND IN 2.8. SO WHAT THE FLYING FUCK IS GOING
ON.I DON'T FUCKING UNDERSTAND. I DON'T. FUCKING. UNDERSTAND. THIS. FUCKING TWISTED CUBIC CURVE. I'M BEING FUCKING STRANGLED. I'M BEING FUCKING STRANGLED, FOR FUCK'S SAKE. I CAN'T FUCKING DO THIS.
I'M FUCKING MOVING ON. IF ANYONE CAN SEE MY MISTAKE, PLEASE LET ME KNOW (YES I'LL FINALLY UPDATE MY ABOUT PAGE IN A FEW DAYS). OTHERWISE, I'M JUST GOING TO MOVE ON TO THE NEXT FUCKING EXERCISE. MAYBE THE NEXT TIME I SEE THE FUCKING COCKSUCKING TWISTED CUBIC CURVE, I'LL JUST SKIP IT. I CAN'T FUCKING TAKE THIS ANYMORE. NOT TONIGHT. I SPENT THE ENTIRE DAY THINKING ABOUT THIS AND I KEEP FUCKING COMING TO THE FUCKING CONCLUSION THAT THE F2 IS EXTRANEOUS. FUCK THIS.
I'M.
FUCKING
MOVING
ON
FUCK