(S = k[x₀,x₁,…,x_n] in these exercises).

I'm sorry for the hiatus. I've been extremely busy lately. Well, not really. But you know... you're used to these kind of gaps, right? By this point it's par the course. Oh? I see, I see, you missed me. You'd THINK you would have gotten used to it by now, but each time I go on these outings, you can't help but feel the pain of my absence. Shuffling about the house, daydreaming about my face. Lying in bed, alone, with only a picture of me at the bedside to soothe the loneliness a bit. You look at my photographed subtle smile, wishing I was there with you, noticing the blemish on my cheek, blushing a bit, and, feeling a little guilty, your hand slowly crawls down towards your nether regions...

Anyway, this exercise is supposed to be very simple, but it confused the ever living fuck out of me. The main issue is getting confused about whether I'm working in projective or affine space, especially in an exercise that involves both. A good mathematician, given a "point" P = (x₀,x₁,…,x_n) would be able to interchangeably use this "P" in both projective and affine space and understand where he's at (wombo combo hurr durr). In fact, this is what the book does. HOWEVER, I suck. And trying to be clever like this fucked me in the ass. So let's not be clever and make things explicit.

What is projective space? Pⁿ is just (Aⁿ⁺¹ - 0)∕ ~ where (x₀,x₁,…,x_n) ~ (cx₀,cx₁,…,cx_n) where c≠0. Letting π : (Aⁿ⁺¹ - 0) → Pⁿ be the quotient morphism, I'll denote π(P) = [P]. So, e.g. a point Q ∈ Pⁿ is actually Q = [P] for a point P ∈ Aⁿ⁺¹ - 0, where [P] = [cP]. PHEW. *Wipes forehead*.

One more thing to get things explicit: I'll reframe another definition in the book in this notation. That is, for a homogenous polynomial f ∈ S and [P] ∈ Pⁿ, we define:

(1)

I.E., for P ∈ Aⁿ⁺¹ where P≠0, we have

(2)

FUCKING. PHEW. *WIPES.* *FOREHEAD.* (had to figure out how to use the \cases environment again)

Now that we've established that cancer. let's unravel the "hint". Let's compute the affine coordinate ring of Aⁿ⁺¹ in Aⁿ⁺¹. I.e. A(Aⁿ⁺¹) = k[x₀,x₁,…,x_n]∕I(Aⁿ⁺¹) = This is getting tedious = S∕I(Aⁿ⁺¹) = S∕(0) = S. *WIPES MOTHERFUCKING FOREHEAD AGAIN*. (I should already know that the coordinate ring of Aⁿ⁺¹ is S. In fact, I had a whole fucking speech about it in an earlier post. Woops).

Okay, now are we ready to rumble? The point is that Pⁿ and Aⁿ⁺¹ share the same coordinate ring, S, so we can use the normal Nullstellensatz (below) to prove this so-called "homogenous Nullstellensatz".



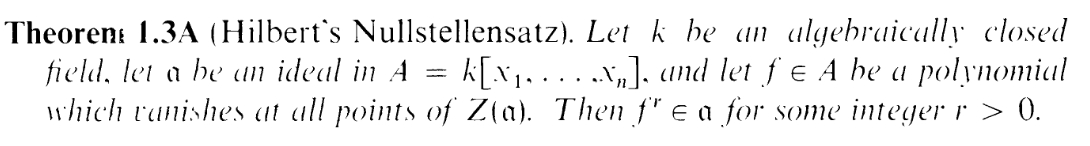
Now suppose α is a homogenous ideal. I.e. it is generated by homogenous elements which I'll denote f₁,f₂,… (actually, according to the book because of Noetheriannness it's generated by finitely many homog elements, but there's no need to use that fact for this exercise. I'll keep it general). And suppose we have f as given in the exercise. We need to show f^q ∈ α for some q > 0.

Okay... one more "expletive" (FUCK!) to make this clear:

When we say Z(α) we could either be taking the zero set in projective or affine space. So when I'm taking it in projective space, I'll denote it Z_P and for affine space I'll say Z_A (don't worry, I am using macros to not turn this into the syntax olympics). so the f we're given here satisfies f(P) = 0,∀P ∈ Z_P(α). To apply the regular Nullstellensatz we basically want to replace the Z_P with Z_A.
Okay, NOW, we're done with the explicitizing. *FOREHEAD WIPE MARK IV*

CONSIDER, dear reader, an element Q from Z_A(α).

CASE 1: Q≠0:
A point being in the zero set of an ideal is equivalent to it being zero on the ideal's generators. I.e. we have f₁(Q) = f₂(Q) = = 0. Now since Q≠0, we can consider its projective equivalent, [Q], and by (2), f₁([Q]) = f₂([Q]) = = 0. I.e. [Q] ∈ Z_P(α). Hence. we know that f([Q]) = 0. But by (2) again, this means that f(Q) = 0. CASE 1 DONE.
CASE 2: Q = 0:
One thing that was initially very confusing to me was why the deg f > 0 assumption is necessary. It's not in the original Nullstellensatz, so why is it included here? This case explains why. We can't convert Q to a projective point like in case 1 because Q = 0. BUT, since f is assumed to be homogenous with positive degree, f(Q) = 0 automatically. So there it is. CASE 2 DONE.

What have we shown? We've shown that for any Q ∈ Z_A(α),f(Q) = 0. I.e. we've satsified the conditions of the regular Nullstellensatz. Hence, f^q ∈ α for some q > 0. So we're done.

*le forehead wipe.*

Since the deg f > 0 thing was so confusing to me at first, I actually did some extra analysis of it (and it's sorta related to the next exercise, so might as well write this down). How does the theorem break if deg f = 0? Consider e.g. f = 1. and let's work in P², and let α = (x₀,x₁,x₂). Then Z_P(α) = ∅ (since we'd need a point to be all 0 to satisfy this constraint). So f vacuously fulfills the condition for this Nullstellensatz (the ∀ symbol iterates over an empty set), but f^q is not in α for any q. So the theorem breaks in this example.

However, it doesn't ALWAYS break for deg f = 0. E.g. if f = 0 (if you consider 0 to be a degree 0 element...). then f is automatically in any ideal, so the theorem holds. Or take f≠0 but make α = (1) (certainly a homogenous ideal). Then, again Z_P(α) = ∅ so the condition is vacuously satisfied, but f ∈ α trivially, so the result holds.

These edge cases gave me a lot of confusion in the upcoming exercises, so I decided to lay some of them out here to help myself moving forward, lol.

I have not proofread this too closely, and I suspect I made some typos/mistakes. Soz.

MISC: For some reason, the "make4ht" command wasn't completely understanding my \newcommand macros at first, but I followed this advice and that fixed it.