This post is mostly straight math. Feel free to skip this post if you only like squiggly math.

SOME NOTES TO MYSELF BEFORE BEGINNING:
I covered some of the cases of Z(α) = ∅ in the previous post. Note that, in (ii), the = S case DOESN'T break the homogenous Nullstellensatz, whereas the = S ₊ COULD break the homogenous Nullstellensatz.

Also, in the previous post, I supposed that the degree of 0 in S = k[x₀,x₁,…,x_n] ought to be 0. Oddly, it appears that this isn't the case. It appears that 0 transcends degree. See condition (ii) in this exercise. The ideal 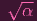can be equal to S₊, which contains NO zero degree elements. And yet, since is an ideal, we must have 0 ∈ i.e. 0 ∈ S₊. So 0 is in the positive degree part of S. However. S₀ itself is the same as k, and certainly 0 ∈ k. so 0 ∈ S₀. So it's in the zero degree part of S as well. SO, basically, you can't put a degree on 0. I'll keep that in mind, I guess.

OKAY NOTES FIN. LET'S BEGIN.

(i) (ii):

Let f ∈ S be homogenous positive degree. Then vacuously ∀P ∈ Z(α) : f(P) = 0 (since (i) says Z(α) = ∅). By the homgenous Nullstellensatz (2.1), f^q ∈ α for some q > 0 i.e. f ∈ .

Thus, we've established that S₊ ⊂ .

CASE 1: 1 ∈ α
Then α = S.

CASE 2: 1α
Then certainly 1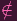 (else 1^q = 1 ∈ α, a contradiction). But if 1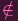 then c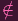 for any nonzero constant c ∈ k (otherwise we'd have c⋅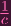 = 1 ∈ α, a contradiction). I.e. ∀c ∈ S₀ : c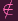 . So must be contained in S₊. I.e. ⊂ S ₊.

DONE.

(ii) (iii):

CASE 1: = S
Then 1 ∈ , which means that 1^q ∈ α for some q, but this just means that 1 ∈ alpha i.e. α = S. But S ⊃ S_d. CASE 1 DONE.

CASE 2: = S ₊:
Suppose THIS were true:

(1)

(we're working in Pⁿ by the way lol)
(also, shouldn't have used k cause that usually refers to the field but fuck it too late lol)
Then for d = k(n + 1), consider S_d.
Let cx₀^k₀x₁^k₁x_n^k_n be an arbitrary term of S_d.
We have to have k₀ + k₁ + + k_n = d, which means that we have to have k_i >=k for at least one i. Assume without loss of generality that i = 0. Then we can rewrite that arbitrary term by factoring out an x₀^k:
x₀^k(cx₀^k₀-kx₁^k₁x_n^k_n)
But this guy is actually in α, since x₀^k ∈ α (by (1)) and x₀^k ⋅ f ∈ α for any f ∈ S (since α is an ideal). So we basically showed that an arbitrary element of S₀ is in α. I.e. we showed S₀ ⊂ α.
To finish off case 2, we just need to show that (1) is true. Since = S by assumption, we must have x₀,…,x_n ∈ . I.e. for each i = 0,…,n, we have x_i^m_i ∈ α for some m_i > 0. But then certainly x_i^{m₀m₁m_im_n} ∈ α. (e.g. (x₀^m₀)^m₁m_n ∈ α, etc.).
CASE 2 DONE.

(iii) (i):

We're given α ⊃ S_d. Taking Z(⋅) of both sides, we reverse the inclusion, yielding

(2)

But since x₀^d,x₁^d,…,x_n^d ∈ S_d, a point P would have to be all 0 in order to be 0 at all of these (since k is an integral domain!) and this can't happen in Pⁿ, so we actually have Z(S_d) = ∅. So by (2), Z(α) ⊂∅ i.e. Z(α) = ∅.