I.1.1c
3/23/2021
SEEYA IN SECTION 3 (it'll take a few days for me to read through it, so you can relax for a bit
from my pink assault). The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a
special case of the ellipse, though historically it was sometimes called a fourth type.
WELCOME BACK TO SECTION 1, SUCKERS. Yes, we are returning back to the very first exercise to unstar a
star. To deface a diva.
And therein lies another lie: the elongation of few into nine. Ten, actually, but it didn't rhyme. Have you relaxed?
Are you relaxed? Some of you may have been edging the whole time, waiting for Hartshorned to give you a release.
And, if you
are, listen: stay with me, buddy. Don't let it out yet. Read through my post and at the very end I'll give you
cumming permissions. Look at me. *Grabs your shoulders* LOOK AT ME. This is your only chance to do so.
Once you've read this post once, the spontanaeity of the interaction will have been exhausted and
there is nothing to have sex with but spent souls. DON'T YOU UNDERSTAND THE SEVERITY
OF THIS SITUATION. "u kno wish I cood experience _____ for the first time again (T_T)." <—–
DONT LET THIS BE YOU, GODDAMNIT. I CARE ABOUT YOU BABY. I DON'T WANT TO SEE
YOU FALL.
To open your mind a bit, here's a treat: What are the different types of conic sections?
Parabola, hyperbola, ellipse, eh? You think that's an apt classification here in these parts? Hey, fuckface: You know
where you are? Yeah, we're in alg geo over k alg closed. Ellipses and hyperbolas are, like, the same thing. Don't look
at me, look at the writing on the screenshot of the pirated pdf. At the end of 3.1a I will tell you that an ellipse is
isomorphic to a hyperbola, and you will kneel.
Now, a general conic has the form
| f = Ax2 + Bxy + Cy2 + Dx + Ey + F, | (A,B,C not all zero) |
(as the exercise states, we're assuming f is irreducible)
Now, this form is super inconvenient, as I learned by struggling for an entire day. Given f, I'd like to convert it into one of the following standard forms
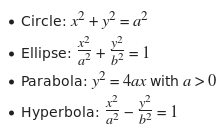
And this can apparently be done via a mere "rotation and translation of axes". Now here's the question: Do I get an isomorphic coordinate rings by rotating and translating axes? If W = Z(f) (f irreducible) and W′ = Z(f′) is the conic defined by rotating and translating W, is it the case that A(W) ≃ A(W′)?
Intuitively, the answer is yes, duh, but you know what they say: TO USE IT, YOU HAVE TO PROVE IT – a rule that I've broken 3000 times on this blog, and yet for some reason I decided to go all the way this time.
Let's work this out. Here's a little lemma to help me:
LEMMA 1:
If ϕ : A → B is a ring isomorphism, and I is an ideal of A and J = ϕ(I), then ϕ induces an isomorphism A∕I ≃ A∕J.
PROOF:
See here: https://math.stackexchange.com/a/2151542.
LEMMA 1 FIN.
Now, let's show the translation thingy in a fairly general setting:
LEMMA 2 (translation):
Let X be an algebraic subset in An.
Given T = (T1,…,Tn) ∈ An,
Let Y = X + T = {P + T|P ∈ X} be the set X translated by T.
Then A(X) ≃ A(Y )
PROOF:
Given f ∈ k[x1,…,xn], let's find the corresponding polynomial for the translated points: Let
| fT | = f(x1 - T1,…,xn - Tn) |
So clearly
 |
And thus, I(Y ) = (fT|f ∈ I(X)) (the ideal generated by the fTs)
Now I want to show that
| A(X) | ≃ A(Y ) | ||
| i.e. k[x1,…,xn]∕I(X) | ≃ k[x1,…,xn]∕I(Y ) |
To do that, I'm going to make a k-algebra morphism:
| ϕ : k[x1,…,xn] | → k[x1,…,xn] | ||
| xi |
 xi - Ti xi - Ti |
Which, clearly, is an isomorphism with ϕ(I(X)) = I(Y ). Hence applying LEMMA 1 finishes us off.
LEMMA 2 FIN.
Now for rotations. Actually, you know what? I'm going to include reflection as well. No, no. I can get even more general: I can make this work for ANY INVERTIBLE LINEAR TRANSFORMATION.
Check this out:
LEMMA 3 (linear transformation):
Let X be an algebraic subset of An.
Given Q an invertible matrix,
Let Y = QX = {QP|P ∈ X} be the image of X under the linear transformation Q
Then, A(X) ≃ A(Y )
PROOF:
Again, given f ∈ k[x1,…,xn], I'd like the corresponding polynomial for the linearly transformed points.
To keep things general, let's just consider an arbitrary invertible matrix A.
What's the corresponding polynomial for the points transformed under A? Like in the translation case, to get the polynomial for the transformed set, I need to apply the inverse of the transformation on the coordinates. This time, let me use k[x1,…,xn] for the original coordinates and k[x1′,…,xn′] for the new coordinates. And let me write x = [x1,…,xn] for the vector of indeterminates in the original coordinate system, and x′ = [x1′,…,xn′] for the vector of indeterminates in the new coordinate system. Then the transformation can be expressed as x′ = Ax. But I want the old coordinates in terms of the new coordinates (since I want to translate f to the new coordinate system). So I take A-1 of both sides to write x = A-1x′. Hence, I'll define
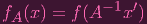 |
So, thinking of x as a point,
| f(x) | = 0 | ||
| ⇐⇒f(Q-1Qx) | = 0 | ||
| ⇐⇒(fQ)(Qx) | = 0 | ||
We can conclude that f(P) = 0⇐⇒fQ(QP) = 0, so the ideal of Y = QX is I(Y ) = {fQ|f ∈ X}
Now to construct the isomorphism for LEMMA 1, I'd like to say is that (fQ)Q-1 = fQ-1Q = fI = f
(the last equality is obvious: fI(x) = f(Ix) = f(x)). So I'm going to one up a bit and prove that in general,
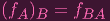 |
This took me 3 days.
We need to actually look inside the matrix. Let's write
| A-1 | =
 |
Note that
| x | = A-1x′ | ||
  | =

 | ||
=
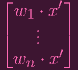 |
So the change of coordinates map is
| ϕA : k[x1,…,xn] | → k[x1′,…,xn′] | ||
| xl |
 wl ⋅ x′ wl ⋅ x′ |
(If you were confused earlier, this is what I meant by writing the old coordinates in terms of the new coordinates). Note that this defines a k-alg morphism such that ϕA(f) = fA
Specifically,
| fA(x) | = fA(…,xl,…) | ||
| = f(…,ϕA(xl),…) | |||
| = f(…,wl ⋅ x′,…) | |||
Now, let me write B as
| B-1 | =
 | ||
=
![[ ]
| |
c1 ⋅⋅⋅ cn
| |](Ip1p1c12x.png) |
Note that bi,j = cj,i (You'll see why I included the column vectors soon enough). And the map for B (let's use coordinate rings k[x1′,…,xn′] → k[x1′′,…,xn′′] for B) is:
| ϕB : k[x1′,…,xn′] | → k[x1′′,…,xn′′] | ||
| xl′ |
 bl ⋅ x′′ bl ⋅ x′′ |
Showing that fBA = (fA)B is equivalent to showing that
 |
and it is sufficient to show that on the generators xl
Now, recall that
| fBA(x) | = f((BA)-1x′′) | ||
| = f(A-1B-1x′′) |
In particular,
| A-1B-1 | =

![[ | |]
c ⋅⋅⋅ cn
1| |](Ip1p1c16x.png) | ||
=
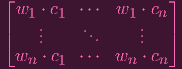 |
So the map representing BA looks like
| ϕBA : k[x1,…,xn] | → k[x1′′,…,xn′′] | ||
| xl |
 wl ⋅ c1 ⋅ x1′′ + wl ⋅ c1 ⋅ x1′′ +
 + wl ⋅ cn ⋅ xn′′ + wl ⋅ cn ⋅ xn′′ | ||
| = ∑ j=1nwl ⋅ cj ⋅ xj′′ |
My goal is to compute ϕB ∘ ϕA(xl) and check that I get the same thing:
| ϕB(ϕA(xl)) | = ϕB(wl ⋅ x′) | |||||
| = ϕB([wl,1,…,wl,n] ⋅ [x1′,…,xn′]) | ||||||
= ϕB(wl,1 ⋅ x1′ +
 + wl,n ⋅ xn′) + wl,n ⋅ xn′) | ||||||
| = ϕB(∑ i=1nwl,i ⋅ xi′ | ||||||
| = ∑ i=1nwl,i ⋅ ϕB(xi′) | (ϕB a k-alg morphism) | |||||
| = ∑ i=1nwl,i ⋅ bi ⋅ x′′ | ||||||
| = ∑ i=1nwl,i ⋅∑ j=1nbi,j ⋅ xj′′ | ||||||
| = ∑ i=1n ∑ j=1nwl,i ⋅ bi,j ⋅ xj′′ | ||||||
| = ∑ i=1n ∑ j=1nwl,i ⋅ cj,i ⋅ xj′′ | ||||||
| = ∑ j=1n ∑ i=1nwl,i ⋅ cj,i ⋅ xj′′ | ||||||
| = ∑ j=1nwl ⋅ cj ⋅ xj′′ | ||||||
And thus, we are fucking done. using the isomorphism (now ignoring the primes on the coordinate rings)
| ϕQ : k[x1,…,xn] | → k[x1,…,xn] |
(It's an isomorphism because, as I showed, ϕQ-1 is two-sided inverse for it), clearly ϕQ(I(X)) = I(Y ) (since for any f, fQ = ϕQ(f)). Hence, LEMMA 1, finishes off the proof.
AND THAT'S LEMMA 3 FOLKS
Reader, if you're still edging, Godspeed. Now we finally get to do the actual proof. Indeed: We haven't even started the actual proof. Reminder? Those lemmas were meant to just let me rotate and translate the conics (and yes, they took me three days to prove). Now I get to translate and rotate them and start actually doing the exercise. You know what they say: If you're edging, keep edging. Woops, I meant: If you use it, prove it.
Now, given an irreducible quadratic f, I can translate and rotate it so that it fits one of the standard forms:
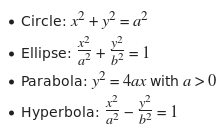
However, using LEMMA 3, I can simplify things even further. Using the change of basis matrix
![[a 0]
0 a](Ip1p1c21x.png) I can
assume a = 1 in the circle equation. Using
I can
assume a = 1 in the circle equation. Using
![[ ]
a 0
0 b](Ip1p1c22x.png) , I can assume a,b = 1 in the ellipse equation. (So really, I can
merge the circle and ellipse cases into x2 + y2 = 1. Similarly, I can rotate and stretch the parabola to be y = x2.
And finally, I'll rotate and stretch the hyperbola to be xy = 1. Hence, here are my new equations:
, I can assume a,b = 1 in the ellipse equation. (So really, I can
merge the circle and ellipse cases into x2 + y2 = 1. Similarly, I can rotate and stretch the parabola to be y = x2.
And finally, I'll rotate and stretch the hyperbola to be xy = 1. Hence, here are my new equations:
| Circle: x2 + y2 = 1 | ||
| Parabola: y = x2 | ||
| Hyperbola: xy = 1 | ||
Any conic can be reduced to one of those (up to isomorphic coordinate ring). Now I'm going to merge the Circle and Hyperbola cases into one to finish the exercise, and so that you can finish along.
Now, I'd like a k-algebra morphism
| ϕ : k[x,y] | → k[x,y] |
To be an isomorphism mapping xy - 1 to x2 + y2 - 1. In which case I can apply LEMMA 1 and be done with this exercise.
To make a k-alg morphism, I need to figure out what x and y should map to. I decided that perhaps the easiest way to do this is to make it my goal to map xy to x2 + y2. I need x to map to a "component" of x2 + y2 and y to map to another "component" of x2 + y2. In other words, I need to FACTOR x2 + y2 into something like SṪ, so I can decide to map x
 S and y
S and y
 T. But is that even possible?
T. But is that even possible?
Even more, I'd like ϕ to be surjective, so ideally I would have S and T to be both linear polynomials. So, I'd like to factor x2 + y2 = (Ax + By)(Cx + Dy)... But again, is this possible?
Let's give it a shot:
| x2 + y2 | = (Ax + By)(Cx + Dy) | ||
 x2 + y2 x2 + y2 | = ACx2(AD + BC)xy + BDy2 | ||
Hence, we'd need
| AC | = 1 | ||
| AD + BC | = 0 | ||
| BD | = 1 |
Note that if we've decided on A and B, that immediately determines C and D (equations 1 and 3). Now look at the 2nd equation:
| AD + BC | = 0 | |||||
 (AB)(AD + BC) (AB)(AD + BC) | = 0 | |||||
 A2BD + ACB2 A2BD + ACB2 | = 0 | |||||
 A2 + B2 A2 + B2 | = 0 | (Equations 1 and 3) |
Let me set A = 1, then that yields
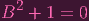 |
Now, reader, if you're edging right now, then hold on for a second. Actually, you know what? Keep going. Keep
going, my strong sailor. but also PAY ATTENTION: This is a VERY IMPORTANT MOMENT: Direct your sexual
energy to focus on this. Let me ask you a question: Does this equation, B2 + 1 = 0 have a solution? Typically, in
your familiar field R of real numbers, this would not have a solution, and our proof would be doomed. But since k
is algebraically closed, this equation is guaranteed to have a solution. E.g. for k = C the complex
numbers, B = i (the unit imaginary number) is a solution. What I'm essentially saying here is that,
circles and hyperbolas are different beasts over the real numbers. But once you algebraically close your
field, circles and hyperbolas are THE SAME. At least by algebraic geometry standards. (Well, in this
exercise, I'm showing that their coordinate rings are the same, but I'll give you the goods in 3.1a)
So, basically, I can factor x2 + y2 = (Ax + By)(Cx + Dy). And since I set A = 1, I know that C = 1, so I
can just write x2 + y2 = (x + By)(x + Dy). Also note that B≠0, since 0 can't be a solution to
B1 + 1 = 0 (we're assuming 0≠1 in k). So also D≠0. One thing I'll also note is that B≠D. Otherwise
AD + BC = 0
 AB + BC = 0
AB + BC = 0
 1B + B1 = 0
1B + B1 = 0
 2B = 0
2B = 0
 B = 0, a contradiction.
B = 0, a contradiction.
THUS, I would like to define ϕ as follows:
| ϕ : k[x,y] | → k[x,y] | ||
| x |
 x + By x + By | ||
| y |
 x + Dy x + Dy |
It's a k-alg morphism that's "clearly" injective (EXERCISE LEFT TO READER... AFTER I LET YOU CUM), so I just have to verify surjectivity. In other words, I have to verify that x and y are in the image of ϕ.
Note that
| x - y |
 (B - D)y (B - D)y | ||
 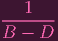 (x - y) (x - y) |
 y y |
(that logic works since I showed earlier that B≠D)
Also note that
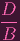 x x |
  (x + B)y (x + B)y | (Since B≠0) | ||||
=
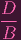 x + Dy x + Dy | ||||||
  x - y x - y |
 ( (
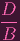 x + Dy) - (x + Dy) x + Dy) - (x + Dy) | |||||
=
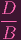 x - x x - x | ||||||
= (
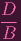 - 1)x - 1)x |
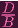 - 1 = 0
- 1 = 0

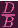 = 1
= 1
 D = B, a contradiction. So
D = B, a contradiction. So
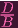 - 1≠0, and we can thus write
- 1≠0, and we can thus write
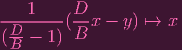 |
HENCE: ϕ is surjective and we're done!
YAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAY. So hyperbolas
and circles (and ellipses) have the same coordinate rings (over k alg closed). In exercise 3.1a, I'll tell you that this
does in fact mean that a hyperbola and circle are isomorphic (over k alg closed): They're "the same", by alg geo
standards. SEEYA IN 3.1a. Also, you can cum now.