II.3.10
3/21/2022
Ahhhh, it’s foggy up here alright. Their Rade promenade is GLORIOUS, and
ours is all the reputable breaking down under pressure, leaders arguing
amongst themselves. March of the losers. The Alps boys picked off the
earlier ports so trivially, but this one here’s like a whole different ball
game. Forces concentrated in coalition in the crescent, carronades peering
down from the upper decks. T-w-e-n-t-y-t-w-o-o-f-t-h-e-m. What are we
gonna do? WTF IS GOING ON? Boy you look like youve seen a ghost,
hahaha. Or a three decker in the smoke. No one wants to even try em.
We’re way in over our heads. We got overconfident due to a lucky streak,
but now we’re dealing with the real $hit. We’re gonna frigging die, bro.
I wanna go home. I wanna go home, home. I can’t stand myself. I can’t do
anything on my own. I don’t know how to exist. I don’t know what’s going on. I
regret coming up here. I shouldve been a coward. I shouldve known I wasnt
capable of this. I cant even do the basic stuff. I cant take care of myself. Im falling
behind on every task. And no one has a clue yet. When they find out, it’s all over.
Theres no forgiveness here. Everyone here acts like theyre your friend but theyll
be the first to testify against you and behead you as soon as they find out
youre slacking. I never made any real friends. What am I supposed to
do? They woulda beheaded me had I dodged, so I was screwed either
way. I cant believe it. I was never meant for great things after all. I grew
up to be a complete failure and there’s gonna be no comeback. I mean
Ive said that over and over to be edgy but now looking over the naval
harbringers of my imminent death, I cant believe its all going to be over. Im
legit gonna die. All my dreams are going to end here. I can’t believe I
spent the two decades of my life doing nothing. Now it’s all going to go to
waste. But you know what? I don’t even have any dreams anymore. I just
want to be safe from all this smoke and fire. That’ll be enough. I want
my future to be a bright spread of fantasy, and not shamefully tucked
behind me. I’m not gonna make it. Someone help. Help. Help. Help me
please. I don’t know what I’m doing. I can’t do it. I wanna go home.
I wanna go home. I wanna go home. I wanna go home. I wanna be a
kid again playing with dolls. I don’t wanna streak my home all up with
blue white red, get sent on these dubious campaigns. I dont really care
about all these abstract principles we’re fighting for. Fuck revolution. Fuck
chaos. Fuck collapse. Fuck anarchy. Fuck primitivism. Fuck bread. Fuck
Communism. Fuck the chants. I just wanna be home again. I wanna be safe
again. I wanna be warm in pajamas by the fireplace, playing war on the
carpet lying down, warm, warm. I wanna be under a blanket, wake up
to an alarm and have the liberty and justice to snooze it out hour by
hour, waking up each time with the comforting thought that i get to drift
back into sweet sleep. I wanna be comfy again. I wanna be happy again.
THE WEATHER OUTSIDE IS FRIGHTFUL, BUT
THE FIBER IS SO DELIGHTFUL♪ Yes, it’s foggy
out here alright. It’s awful, unforgivingly rude to the aim. There's no friendliness up here in the elements nor the representatives. It's cruelty unabated. Well you’re still a itsy
bitsy boy to me yknow. You can come to me even over the stupidest things, like a
booboo on your cheek and I’ll kiss it like a doting wife. BTW, the Spanish don’t
trust the British, and them Neapolitans are stubborn. Aint no such thing as a
”strong coalition.” The offseason mistral plucked off two of their 2nd rates two
days post landing. And then there’s the city, divided among itself. It’s
always offseason for you out here, rite? That’s your edge. Dirtied, base, and
bellowing in elan, all only want of direction by wit. Then lemme show you the
ropes, and make you one of the early few that can catch a worm: Take the
prolonge with your hands, I’ll wrap mine around yours, and together we
pullback. The third wheel nestles into the rail. Ahh, I love the sound of that
click, cause I know I’m about to raise hell. Yea the gauge on an old iron
baby’s just a crude ass notch, A RESIDUE OF A DUMBASS’S AXE
SWING, but your peers will be all the more impressed at your kill count. As well
as the enemy. Ye shall be: The Ghost of Coast (LMFAO). Aim
where the ship’s gonna be, not where it is. Yes, you’ll get the hang of it.
It seems impossible at first, and you will struggle and miss, and miss,
and miss, and miss, but you’ll find your coastal knack soon. Y’see, half
the trick is believing itll work. The way to carry yourself thru life isnt
self-esteem or self-love, but self-trust. Ah yes, it’s frightfully foggy today. But
for now you’re in good hands: Grab the handspike, and I’ll envelop you
from behind, motioning the turn of the cannon. How does one aim in the
fog? If you wanna shoot arrows from one scheme to
another, if you wanna punch ugly holes in beautiful ships, you can break it
up fiber by fiber. Because that’s all a rope is: A bundle of fibers, to be
released in a timely fashion. To get the hang of it, stop hanging on, lest
you hang a la lanterne. You wanna stay alive, right? Now it’s out of your
hands, and mines out of yours. You’ll be lucky in this Army to maintain a
motley 8 and old machine. It’s cold, with intermittent blasts of warmth
which only make you long for more. Let it go. Childhood is dead, and the
Rade ahead is lonely. Trust your companion to time the ignition, and
AS LONG AS YOU LET HER GO, LET IT
BLOW, LET IT BLOW, LET IT BLOW♪
1 Prelims
Let’s talk about residue fields, and establish some conventions.
1.1 Residue fields
First of all, as the Wikipedia page states, for a local ring R, the residue field is
R∕𝔪. And when you have an arbitrary ring A, you can localize at a
prime ideal P to obtain the local ring AP. The maximal ideal of this
ring is PAP, so the residue field of AP is A∕PAP. This would also be
considered the residue field k(x) of the scheme SpecA at the point x = P.
One very crucial fact missing from that page is this equality:
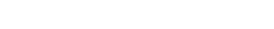 |
So when I take a residue field, I may use the former or latter representation,
depending on what’s more convenient.
1.2 A useful quotient
When it comes to polynomial rings over k, here’s a useful related isomorphism (I think k needs to be algebraically closed, which Hartshorne lets us assume in this exercise):
| k[x1,…,xn]∕(x1 − a1,…,xn − an) | ≃ k | ||
| xi |
 an an |
1.3 muh notation
And by the way, if A is a B-module, and b1,…,bn ∈ B, it’s a valid question
whether by (b1,…,bn) I mean the ideal generated by those elements in
B or in A. They are different ideals, but often times I will abuse this
notation and silently convert it from one ideal to the other when it just works.
3.10

Now here’s the fiber of a morphism:

A morphism of scheme can be broken up... into schemes. I wouldn’t be able to tell
you why it’s defined as the domain scheme fiber producted with the residue field
of the target scheme. BUT, I did tell you last time how to compute fiber products:
Indirectly.
A

So, to clarify: The only reason we’re not saying that Xy is isomorphic to f−1(y)
is that there is not necessarily an established scheme structure on f−1(y)
(especially if it’s neither open nor closed in X). If nothing, this exercise tells us
we can induce the scheme structure of Xy onto f−1(y). So yes, if you’d like,
f−1(y) ≃ Xy as schemes. But in that case, showing that they’re
homeomorphic is sufficient.
We are computing
| Xy | = X ×Y Speck(y) |
General products of schemes can be obtained by gluing together affines. So I’ll
assume without loss of generality that X,Y are affine, with X = SpecA and
Y = SpecB. In which case, we are computing
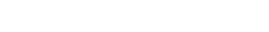 |
AGAIN, FOLLOWING OUR LESSON FROM LAST TIME: DEAL WITH THIS
INDIRECTLY. Do NOT try to jump into the ring and try to do tensor math. In
fact, we’re going to be even more abstract and indirect than last time.
Tensoring is right exact. Hmmm? Right exact? So what? Who cares about
functors and all that nonsense? Well, we do. Tensors aint pretty close up, so we’re
zooming out to deal with it. Don't aim where the ship is, but where its gonna be. We’re gonna hide the tensor under something else,
and it begins with this right exact sequence:
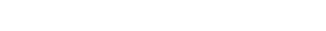 |
Now we tensor it:
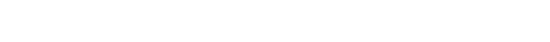 |
The second last arrow, of course, is surjective. Hence, there is a bijection
between prime ideals of R and prime ideals of A ⊗BBy that contain
ker δ = imλ = A ⊗ByBy.
Now if you do dive into A ⊗BBy, you might find something strange: That this
tensor product seems to effectively be, simply, a sort of structure on A. In fact,
this tensor product is just another way of localizing A at S = B − y:
 |
There goes the tensor! Yaaaay! Bye bye! Now we are going to produce a string of
equivalences:
Instead of looking for ”the prime ideals of A ⊗BBy that contain A ⊗ByBy”
we are looking for ”the prime ideals of S−1A that contain yS−1A.” But these
are just ”the prime ideals of A that contain y but do not intersect S = B − y”
which are precisely the prime ideals of that are mapped onto y from B under the
B-module structure on A, i.e. f−1(y).
These ”bijections” are all given by ring morphisms, so they do in fact induce
homeomorphisms.
B
A lot of text here, but it has a very simple picture which you might already be
able to start making out.
When Hartshorne talks about the point y ∈ Y as a ∈ k, he means y is the
maximal ideal (s − a) in Y = Speck[s]. Now since from part A, we know that
Xy = f−1(y), the question is, given the map
| ϕ : A = k[s] | → B = k[s,t]∕(s − t2) | ||
| s |
 s s |
which prime ideals of B have an inverse image of y = (s − a)? To make this
easier, let me decompose ϕ:
![ϕ : k[s] `→δ k[s,t] ↠λ k [s,t]∕(s − t2)](IIp3p107x.png) |
So seeing k[s] as a subring of k[s,t] and using the isomorphism theorem, we
are simply looking for the prime ideals of k[s,t] that contain (s − t2)
and whose inverse image under δ is (s − a). Hold on, what’s this δ?
| δ : k[s] | → k[s,t] | ||
| s |
 s s |
But now let’s bring up the birb in the room. Aren’t those very, very familiar
rings? If we Spec it, we just get
| g : Ak2 | → A k1 | ||
| (S,T) |
 S S |
A good old varietyland map: Projection onto the s axis.
The question is now just ”which points on the curve s = t2 map to s = a under
this projection onto the s-axis?” Or, alternatively: ”What is intersection of the
curves s = t2 and s = a”? Of course, these would just be the points (a,
 )
and (a,−
)
and (a,−
 )
. (
)
. (
 is defined because Hartshorne tells us that k is algebraically
closed):
is defined because Hartshorne tells us that k is algebraically
closed):
Or in the case of a = 0:
YEP, LOL. ALL WE’RE DOING IS INTERSECTING A
PARABOLA AND A LINE.
Well, we’re about to analyze the relationship between a parabola and line more
deeply than we ever have before: We’re gonna look at these points’ structure
sheaf and residue fields. And even those of the mysterious generic points.
Xy’s global section
Let’s go ahead and get a good expression for the ring corresponding to Xy. We’ll
sorta retrace our steps. Recall this right exact sequence:
 |
That last arrow tells us that:
 |
And the left hand side, as we just argued, can be expressed as
 |
Localization commutes with quotients, so this is just
 | (1) |
Now let’s expand this a bit. Note that y is the ideal generated by s−a in B, so
yA is just the ideal (s − a) generated by s − a in A (here’s where I’m being
kind and explaining it instead of waving it away with muh notation). Therefore
| S−1(A∕yA) | = S−1[(k[s,t]∕(s − t2))∕(s − a)] | (2) |
| = (B − y)−1[(k[s,t]∕(s − t2,s − a))] | (3) |
That is the global section for Xy, where y = (s − a). It is the ring whose
spectrum is Xy.
1.3.1 Residue fields of the ordinary points
As discussed, the points of Xy are only in the form (s − a,t −
 )
. So,
using the global section, let’s compute the residue field at this point.
)
. So,
using the global section, let’s compute the residue field at this point.
We are localizing at (s − a,t −
 )
, which is the multiplicative
subset T = k[s,t] − (s − a,t −
)
, which is the multiplicative
subset T = k[s,t] − (s − a,t −
 )
, which clearly contains
S = B − y = k[s] − (s − a), so we can ignore the S once we localize:
)
, which clearly contains
S = B − y = k[s] − (s − a), so we can ignore the S once we localize:
![2 √ --
(k [s,t]∕(s − t ,s − a))(s− a,t− a)](IIp3p1020x.png)
But we are taking the residue field of this, so we want to quotient by the maximal
ideal:
![√ -- √ --
[(k[s,t]∕(s − t2,s− a))(s− a,t− √a)]∕[(s− a,t− a)(k [s, t]∕ (s− t2, s− a))(s − a,t− a)]](IIp3p1021x.png)
Uhhhhhhhhhhhh.
That's not pretty at all... All that is supposed to end up as just k? Yknow I actually managed to somehow get there
from that expression. But in hindsight it’s easier to use the fraction field
representation:
Frac((k[s,t]∕(s − t2,s − a))∕(s − a,t −
 )) )) | = Frac(k[s,t]∕(s − t2,s − a,s − a,t −
 )) )) | |||||
= Frac(k[s,t]∕(s − t2,s − a,t −
 )) )) | ||||||
= Frac((k[s,t]∕(s − a,t −
 ))∕(s − t2)) ))∕(s − t2)) | ||||||
= Frac((k[s,t]∕(s − a,t −
 )))∕Frac((s − t2))) )))∕Frac((s − t2))) | ||||||
| ≃ k∕Frac((s − t2)) | ||||||
| = k∕(s − t2) | muh notation | |||||
The second last equality follows from 1.2, and in particular, that isomorphism is given
by the following map:
k[s,t]∕(s − a,t −
 ) ) | → k | ||
| s |
 a a | ||
| t |
  |
So the relationship s − t2 = 0 is redundant. Hence
 |
So that’s the residue field of Xy at their only 2 (or 1) points.
1.3.2 The tangent
By the way, according to Hartshorne, in the case a = 0 (when the line is tangent
to the parabola), we’re supposed to get that Xy is nonreduced. If you look at the
global section (3) (which is, by the way, the only section, since Xy is a singleton
in this case), it becomes obvious:
| (B − y)−1[(k[s,t]∕(s − t2,s − a))] | = (B − y)−1[(k[s,t]∕(s − t2,s))] | (4) |
s − t2 = 0 and s = 0, so t2 = 0. t is your nilpotent
1.3.3 Generic points
So we’re all wrapped up with the ordinary points y. Now for the generic
points that cannot be drawn: The ones that, respectively, encompass the
entire s-axis and parabola while mysteriously lying nowhere on them:
AND ONE MOTH IS THE EXTENSION OF ANOTHER? The respects from son
to father pays back in extension: Whence geometric retraction gives back into
algebraic expansion. Yes, there is more freedom sliding along a curve than a line.
We’re concerned with the fiber of the generic point η = (0) ∈ Y . And since f is
induced by s
 s, the fiber is the singleton Xη = f−1(η) = {(0)}. Let’s
compute the global section (the only section, since it’s a singleton)
s, the fiber is the singleton Xη = f−1(η) = {(0)}. Let’s
compute the global section (the only section, since it’s a singleton)
1.3.4 Global section of Xη
Starting from , we write
| S−1(A∕yA) | = (B − (0))−1(k[s,t]∕(s − t2)∕(0)A) | (5) |
| = (B − (0))−1(k[s,t]∕(s − t2)∕(0)) | (6) | |
| = (B − (0))−1(k[s,t]∕(s − t2)) | (7) |
1.3.5 Residue fields of the generic points
The residue field of Y at η = (0) is the fraction field k(s) of k[s]. Now, using
the global section (7) above, let’s compute the residue field of Xη (at its only
point (0)). If we localize at (0), that’s the multiplicative subset A − (0), which
clearly contains B − (0), so that can be dispensed with, and we get
| [(B − (0))−1(k[s,t]∕(s − t2))] (0) | = (k[s,t]∕(s − t2)) (0) | ||||||
| = Frac(k[s,t]∕(s − t2)) | = k(s,t)∕(s − t2) | (MUH NOTATION) |
This is a field, so the maximal ideal is (0), giving us back the same field. What
you see above is the residue field of Xη.
Now we want to show that k(s,t)∕(s − t2) is a 2-degree extension of
k(s). This is quite intereting, cuz we’re tasked with getting a basis for
k(s,t)∕(s − t2) as a vector space over k(s). The quotient is what makes it
work: E.g. s,t (or 1,t) is a generating set. (We can get polynomials in s
through k(s) and we don’t need any higher degrees of t because s = t2)
Done. we’re faking it even here BTW, because we provided no explanation for
the significance of the fact that ”the residue field of the parabola is a 2
degree extension of the residue field of the line when projected onto it.” But we proved it...