I.1.6
12/5/2020

NNNNNNNNOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO.
In all my buccaneering as a wannabe mathematician in years past, I have come across this "fundamental topology
exercise" numerous times. It has some of the basic concepts I'm worst at mixed into one: irreducibility, closure, density.
Ouch, ouch, ouch. It's an insecurity bonanaza, everyone dance! No, I'm not excited. I've done this exercise like probably 5 times, and every time I've
forgotten how to do it, and I struggle all over again. Well, this is part of the reason I started the blog. When I have
to do something like this again, instead of having it hidden in some old notebook, scrawled illegibly over
multiple pages so the logic is impossible to reconstruct, I'll have it written out, here on the web, in a
neater format. It'll not just serve as a reference for future run-ins but as a proud record that I have
conquered it. So, with a function of this blog finally being put into action, I suppose I should be screaming
"YYYYYYYYEEEEEEEEEEEEEEEEEEEEEEEEESSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS", but
I'm more pessimistic than that. Do you remember? Back in 1.1b, I confessed that I had no intuition for
irreducibility. Hey hey, you know how in the last few posts, I got to stroke my chin and ponder the "underlying
purpose" of the exercise, like some inquisitive young student with a future as bright as his mind? This time I have
no idea what the fuck is going on. Even when I finish this exercise, I'll have no idea what the fuck just
happened. My future is as dark as my mind.
Well, let's start with the open set statement. Let U be an nonempty open subset of X, where X is irreducible. The
exercise reads, "dense and irreducible", so in spite of them having switched the ideal order of things on us before,
let's start with density
Let V be a nonempty open subset of X such that V ∩ U = ∅.
Then, complementing both sides (I'm doing this because I know I have to use irreducibility of X, and
complementing gives us an X on the right) we get,
| X - (V ∩ U) | = X | |||||
 (X - V ) ∩ (X - U) (X - V ) ∩ (X - U) | = X | |||||
 X - V = X X - V = X | or X - U = X | since X irreducible | ||||
AAAAAAAAAAAAAAAAAAAAA | ||||||
 V = ∅ V = ∅ | or U = ∅ | taking complements | ||||
Hence U is dense, done.
Now for irreducibility. And boy, I feel like I got fairly "lucky" here, cause I finished the density part first and was thinking of using it, Perhaps a small strain of my past flails at this problem hinted me.
Suppose U = C1 ∪ C2 where C1,C2 are closed in U.
Then C1 = D1 ∩ U, C2 = D2 ∩ U where D1,D2 are closed in X.
Now I define D = D1 ∪D2 (Note D is closed and U ⊂ D). The reason I'm doing this is because I know I have to use irreducibility of X at some point and I'd LIKE D = X. But is that really the case? Let V = X -D, which is open because D is closed. There are two cases
Case 1: V ≠∅
Then V ∩ U≠∅ (since, as we just showed, U is dense!!!!)
i.e. there is x ∈ U such that x ∈ V = X - D
i.e. there is x ∈ U such that x
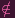 D
DThis contradicts U ⊂ D.
So the unnice case yields a contradiction! YaY!
Case 2: V = ∅
Which translates to the thing I'd LIKE: X = D = D1 ∪ D2.
So then, D1 = X or D2 = X since X is irreducible.
So clearly then C1 = U or C2 = U
Henccccccccccccce U is irreducible. Fuq. That part's done.
NOW, to the second part of the exercise: the closure statement.
Let Y ⊂ X and Y is irreducible in the subspace topology.
Suppose = C1 ∪ C2, where C1,C2 are closed in Y
I know I'm going to use the irreducibility of Y , so lemme intersect both sides with Y , giving
Y = (Y ∩ C1) ∪ (Y ∩ C2)
and since, Y is irreducible, we have Y = Y ∩ C1 or Y = Y ∩ C2.
Assume the first without loss of generality. Taking the closure of both sides,
| = Y ∩ C1 | ||||||
| ⊂ ∩ | See here | |||||
| = ∩ C1 | Since C1 is already closed | |||||
| = C1 | Since clearly C1 ⊂ | |||||
So is irreducible.
Annnnnnnnnnnnnnnnnnnnnnnnnnnd there it is. It did not take me that long. Somehow, unlike past attempts, the proof fell in my lap this time. And this time, I held it in my lap. I pulled my trousers taut and concave up to form a mini-hammock to hold it, and penguin walked it over here to pour it into pink text. Yes: I danced after all, like a chaperone at Homecoming. Yes: Envision me not as a chin stroker but a penguin walker. Do I have any more intuition for irreducibility or what the fuck just happened? No. I'll save my "YYYYYYYYYYYYYEEEEEEEEEEEEEEESSSSSSSSSS"es for more appropriate occasions, if they ever arrive. But right now my pants are wet. Time to change.