I.5.14a
8/28/2021

Hihi reader (sexme). Here's a performance of
Stockhausen's Klavierstuck IX. I actually really like that piece, cause of the
space... and texture... idk music theory. but the part 8:00 till the end makes me
unf. But this comment is also a work of art!
It looks like I have caught up with my notes. Yes, I didn't get that far over my 2
month absence. But we are... "done" with this section. This is the second last
exercise of the section (yes, I skipped 5.13 and haven't even looked at
5.15), and I will PROBABLY just move on (so this is the season finale...
ummm.. does anyone have a less dumb term?). Not only are these last few
disproportionately more difficult, they involve disproportionately more
abstract algebra, which, as we all know, I am terribly unequipped with.
In any case, let's begin. Don't worry: doing algebraic geometry is like
sugar coated jelly pure, unadultered SOVL. Here we go!!!
First, here's your analytically isomorphic definiton bro:
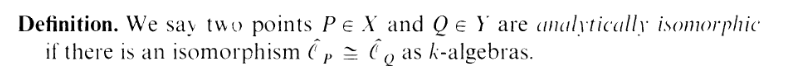 "Err, wtf are those
hats?" Ah, those are just the completions of the local rings, and don't worry, I
have no fucking clue how they work either. Don't worry about it. There's an easier
characterization:
"Err, wtf are those
hats?" Ah, those are just the completions of the local rings, and don't worry, I
have no fucking clue how they work either. Don't worry about it. There's an easier
characterization:
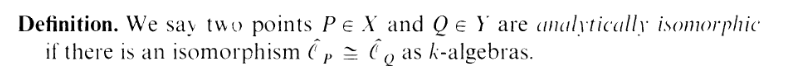 So what do these facts give us? Letting Y = Z(f) and
Z = Z(g), and assuming wlg that P and Q are the origins, we have an
isomorphism like so:
So what do these facts give us? Letting Y = Z(f) and
Z = Z(g), and assuming wlg that P and Q are the origins, we have an
isomorphism like so:
| k[[x,y]]∕(f) ≃ k[[x,y]]∕(g) |
Or, a better way to put it would be to say that we have an automorphism ϕ of
k[[x,y]] mapping f to g.
Now let's break f,g into their homogenous components:
| f | = fs + fs+1 +
 + fl + fl | ||
| g | = gr + gr+1 +
 + gd + gd | ||
I want to show that s = r. Now, here's the thing. Let's say we had any
monomial of, say, degree m. E.g. M(x,y) = axiyj (where i + j = m). And
let's say we map this under ϕ:
| ϕ(M) | = a(ϕ(x))i(ϕ(y))j |
Now, idk if this is necessary, but it's sufficient that as long as ϕ(x) and ϕ(y)
have linear leading forms, then ϕ(M) is going to have a degree of m.
I'm going to call this condition "linear property" for convenience. Let's
assume that automorphisms of k[[x,y]] (like ϕ) satisfy this linear property.
If we now apply ϕ to f:
| ϕ(f) | = ϕ(fs) + ϕ(fs+1) +
 + ϕ(fl) + ϕ(fl) | ||
Remember that fs is made up of degree s monomials, fs+1 is made up of
degree s + 1 monomials, etc. So if ϕ has the linear property, then fs+1 and
higher map to terms with degree above s. And fs? It maps to a polynomial with
a leading form of s, and we're done
..... unless the s degree monomials cancel out LOL. So I should say fs maps to a
a polynomial h with degree ≥ s, but, well, I want equality, obviously. Can I get
it? Answer: Yes. Assume wlg that s ≤ r. Since ϕ is supposed to be an
automorphism, I'd need
| f | = ϕ-1(ϕ(f)) | ||
 fs + fs+1 + fs + fs+1 +
 | = ϕ-1(ϕ(f
s)) + ϕ-1(ϕ(f
s+1)) +
 |
But if deg ϕ(fs) is strictly greater than s, then this equality can't hold.
Because since we're assuming automorphisms satisfy the "linear property",
ϕ-1(ϕ(fs)) has to map to either the same degree or higher (and the other
terms are even more screwed). So we must have equality. Weeeeee! Done!
Buuuuuut. Now we have to show that ϕ does indeed satisfy the "linear property".
Stated more clearly, if
| ϕ(x) | = a0 + a1x + a2y + h0(x) | ||
| ϕ(y) | = b0 + b1x + b2y + h0(x) | ||
We want to show that a0,b0 = 0. (...and also that not both of a1,a2 = 0
and not both of b1,b2 = 0).
Here it is, folks. This is what I spent the "hole day" on. Indeed, this is the fated
moment I had to "look url" for help. Well, I started off on the right track: I
noted that the maximal ideal of k[[x,y]] is (x,y), and since ϕ is an
automorphism of a local ring, it had to map the maximal ideal to itself: We'd
need (ϕ(x),ϕ(y)) = (x,y). I tried proving this directly. I tried. I tried. I tried.
NO luck. So let's look online.
First, note that R is a local ring with maximal ideal m = (x,y), so any automorphism must map m to itself
Muahaha. See? On the right track.
and thus be continuous in the m-adic topology. Since k[x,y] is dense in R in the m-adic topology, this means that an automorphism is determined by where it sends x and y.
.........................
Moreover, given f,g ∈ m, there is a unique continuous
k-algebra homomorphism ϕ : R → R such that ϕ(x) = f and ϕ(y) = g .... So
the only question is what conditions on f and g guarantee that this ϕ is an
automorphism.
The answer is simple: you just need the images of f and g in the k-vector space
m∕m2 to be linearly independent. Concretely, this just means that the linear
homogeneous parts of f and g are linearly independent.
...........................
Clearly this condition is necessary, since the images of x and y in m∕m2 are linearly independent.
......Okay. So putting the topology insanity aside, I kind of get this. a k-algebra morphism of local rings induces (I think) a map of vector space on the corresponding m∕m2 spaces. And if it's an isomorphism, then linear independence must be preserved. OK. Fine.
Now, the rest of the comment covers the "sufficient" condition, and it's interesting and confusing, and I was going to break it down, but I realize that I actually don't need it. I only need the "necessary" part since I'm assuming that ϕ is an automorphism already. So I GUESS WE'RE DONE WTF.
Seeya in the next section! Maybe I should get myself some cake!