I.4.7
6/5/2021
Moving is a very sensitive, complicated process. You have to
make sure you have your finances in order, obviously. And you have to do
extensive research on where you're moving into. There are a lot of questions you
have to ask yourself. For instance: How are the career opportunities there?
You see, where we live is a hotbed of opportunities. Many people are
trying to move here, because this is where all the big name companies are.
People here can go from making nothing to making six figures in just a few
years. If you move into the middle of nowhere, you might be dashing your
opportunities to make it big. Yes, it's expensive here, but that's the price you
pay for living in a safe place. Other places out there might not be as
safe. You don't want to move into a neighborhood with a lot of crime.
And the economy is dynamic. Rent may be cheap somewhere now, but it
might go up later. You have to really study the market before you move.
And, boy, if you're thinking about a rural area, that comes with its own
baggage: You have to be a lot more self-sufficient. You'd better get used to
nature. And you'd better be able to drive. You don't even have a car yet,
do you? The nearest grocery store might not just be simple walk away,
like it is here. And you won't be able to get deliveries very easily either.
And what about weather? Can you deal with the cold? If you're thinking
about the midwest, are you prepared to deal with hurricanes? Moving isn't
something that you can just do on a whim. It's not something where
you can just throw a dart on a map and go there. There's a lot of stuff
you have to take into consideration. A lot of preparation you have to do.
You have to know what you're doing. Some people, they fall into this
nomadic life style. They just move from place to place, never satisfied.
They never settle. And by the time they're in their 30s, 40s, they have
nothing to their name. They haven't built up any career, they haven't held
down a relationship, they've got nothing, all cause they just kept moving
and moving without letting anything develop. My old man was a serial
mover, and he ended up having to work all the way up to his 70s. Imagine
working, except you have like 20 other health problems to also manage. You
don't wanna live that life, do you? What? You don't think you're going to
live that long? What? You don't even think you're going to live past
30? Huh? You don't even assume you'll be alive two years from now?
Wow, dude. I think you might be depressed. That's not a healthy mindset.
Listen man, if you're having issues, don't be shy. I'm here to help. Have
you tried therapy? I dunno, you keep denying it, but that sounds like
depression to me. That's definitely not a healthy mindset. Anyways, my point
is: You need a plan. And you need to compare so many factors before
deciding to move. I'd suggest making a spreadsheet of all the locations
you're thinking about, with all the benefits/costs, like pricing, weather,
gas, etc. and start from there. You see, the thing is, "I just want to get
away from these leafblowers" is not a good reason to move. I understand
that leafblowers are annoying and all, but it just doesn't make sense to
move to a completely different state solely because of them. There's only,
like, 1 hour worth of time in the morning where they go off here. It's
literally just an hour. It's not so bad. There are things out there that are
much worse than leafblowers, I guarantee. I mean, imagine living in a
neighborhood with crime. Would you rather listen to gunshots than leafblowers?
And just in general there's so many more important things to take into
consideration, like career, weather, and all the other stuff I mentioned. Those
are the things you should be thinking about, not something as trivial as
leafblowers. Leafblowers exist everywhere. The place you're moving to could
also have leafblowers, you know? What are you going to do if you spend
all this effort moving because of leafblowers, only to move into a place
with more leafblowers? Move again? I'm sorry, this just doesn't logically
make sense. No matter how I wrap my head around it, it sounds like
you're just coming up with an excuse to move. That's definitely not a
healthy mindset. Have you tried seeing a therapist? I'd highly suggest that
you see a therapist or something, because it sounds like you might be
in the wrong place mentally. I dunno, it just seems you've been a bit
unhinged lately. Listen, mate, all I'm saying is, I don't think it's such a good
idea to move right now, especially with your current mindset. I mean, if
you have a serious reason to move and seriously want weigh all the costs
and benefits, then I'm all up for it. I can fire up Excel and we can start
making that spreadsheet. But I'd honestly hold off on making such rash
decisions till you get yourself together. Just my two cents. 
IT'S MY LIIIIIIIIIIIIIIIFE AND IT'S NOW OR NEVERRRRRRRRRR. I
AIN'T GONNA LIVE FOREVERRRRRR. I JUST WANNA LIVE WHILE I'M
ALIIIIIIIIIIVE. GET OUT OF MY FACE. Listen: I've recovered from yesterday
morning's CIA funded orgy of leafblowers. It was short lived. I went outside, was flanked
by WEEEEEEEEEEEEEEEEEEEAAAAAAAAAAAAAAAAAAAAHHHHHHH
at every corner, and even after it was over, I was so frustrated that it sabotaged
the next few hours. However, by the afternoon, I recovered my default state.
And now, on the next day, I'm thinking back on my silly "I NEED TO
MOVE THE FUCK OUT OF HERE" sentiments. Had I simply stayed
inside during that period of time, I'd have been fine. "I NEED TO MOVE
THE FUCK OUT OF HERE" was just an impulsive, irrational reaction.
Hence, I'm moving cause of the leafblowers, and only the leafblowers. Wait, what?
Yes. You can write "leafblowers" as the impetus on the official records. And
suppose where I end up moving just has more leafblowers? Then I'll move
again. Yes, that's it. Duh. It's simple! Listen: I'm not smart. All your
complicated cost benefit/analysis on making a big decision makes my
brain shut down. I can't think in terms of a spreadsheet. I'm not going
to be able to do something if I actually have to think it through. All
that results in is floundering in indecision like I've been for the past 5
years. I'm not smart enough to figure out the right/optimal/wise/moral
thing. I'm stagnating and running outta time. If you're of my elk, you're
prolly starting to see that it's time to make risky decisions and screw
yourself and maybe even others over, lest you vanish. Listen sister, if you
actually wanna move, for the love of god don't move for a good reason.
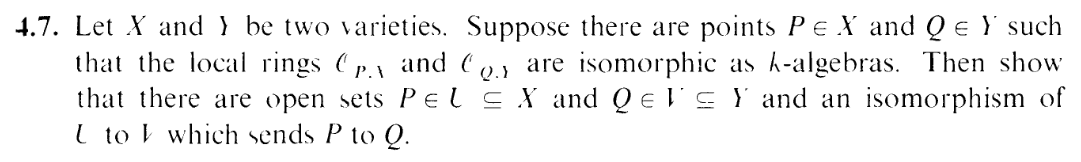
The way I figured this exercise out was by "reverse engineering" it. First note that
we can assume X,Y are affine without loss of generality. Let's suppose I
had a morphism ϕ : X → Y . Then the induced map would look like
ψ :
 P,Y P,Y | →
 Q,X Q,X | ||
| < U,f > |
 < ϕ-1(U),f ∘ ϕ > < ϕ-1(U),f ∘ ϕ > |
Now the key point to note is that we let f be the coodinate functions, we can recover ϕ coordinate by coordinate:
| x1 ∘ ϕ | |||
 | |||
| xn ∘ ϕ | |||
So this is what I'll do.
Let's suppose that we're given ψ, but not such ϕ.
ψ :
 P,X P,X | →
 Q,Y Q,Y | ||
(yea I switched the domain and range from the initial example, sorry lol)
Let X ⊂ An, Y ⊂ Am. And let x1,…,xn be coordinates for An and y1,…,ym be coordinates for Am. Let's consider
| < V i,gi > | = ψ(< X,xi >) | (i = 1,…n) | (1) | |
| < Ui,fi > | = ψ-1(< Y,y i >) | (i = 1,…m) | (2) |
Let U = ⋂ Ui and V = ⋂ V i, and then let
| ϕ : U | → Y | ||
| x |
 (f1(x),…,fm(x)) (f1(x),…,fm(x)) |
(so that fi = yi ∘ ϕ, like it should be). Let's also try making an inverse:
| δ : V | → X | ||
| y |
 (g1(y),…,gn(y)) (g1(y),…,gn(y)) |
Both are obviously morphisms (Lemma 3.6). Now let's show that, where they're defined, ϕ and δ are inverses:
For instance, given x = (X1,…,Xn),
| δ ∘ ϕ(x) | = δ(f1(x),…,fm(x)) | (3) |
| = (g1(f1(x),…,fm(x)),…,gn(f1(x),…,fm(x))) | (4) |
Now look at (1) and (2). And consider gi. Since it's a regular function, it can be written as (in some open set containing P; restrict V as needed) the fraction of polynomials l∕l′ over the yi. And thus
| gi | =
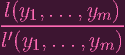 | |||||
 ψ-1(g
i) ψ-1(g
i) | = ψ-1(
 ) ) | |||||
 xi xi | =
 | |||||
 Xi Xi | =
 | (plugged in x to both sides) | ||||
| = gi(f1(x),…,fm(x)) |
Hence, (4) turns into just (X1,…,Xn), which is just x, as needed. So δ ∘ ϕ(x) = x and an analogous argument shows that ϕ ∘ δ(y) = y.
Now I can't yet claim that ϕ and δ are isomorphic, as their domains and images don't necessarily match up. Which is why I said they're inverses where they're defined. Indeed what if ϕ(x) isn't contained in V ? Then δ(ϕ(x)) wouldn't even be defined. But I still need to keep U and V as open sets to satisfy the exercise. So I'll restrict the morphisms like this:
| ϕ′ : U ∩ ϕ-1(V ) | → V | ||
| δ′ : V ∩ δ-1(U) | → U |
Now consider x ∈ U ∩ ϕ-1(V ). Then ϕ′(x) ∈ V . So we can apply δ on this element to get δ(ϕ′(x)) = δ(ϕ(x)) = x ∈ U. So ϕ′(x) ∈ δ-1(U). Which means that imϕ′⊂ V ∩ δ-1(U). Analogous reasoning shows that imδ′⊂ U ∩ ϕ-1(V ). So we can actually write the maps as
| ϕ′ : U ∩ ϕ-1(V ) | → V ∩ δ-1(U) | ||
| δ′ : V ∩ δ-1(U) | → U ∩ ϕ-1(V ) |
Since δ′ is a two-sided inverse for ϕ′, ϕ′ is an isomorphism. Phew.
Last thing: Does ϕ map P to Q? I got stuck here for a while, but I realized that in order to make statements specifically about P and Q, I should use the "locality" of the rings. So let mx and my be the unique maximal ideals of
 P,X
and
P,X
and
 P,Y . The uniqueness follows from the fact that they're local rings, and also
note that they are given by all the elements that are 0 on P (respectively, Q).
Now taking inspiration from example 1.4.4, note that the regular functions
yi - Qi "determine" the point Q. Indeed they are 0 on Q, so yi - Qi ∈ my.
Now where does ψ-1 send < Y,yi - Qi > to? By (2) and basic k algebra
morphism properties, it gets send to < Ui,fi - Qi >. But since ψ-1 is an
isomorphism, it maps maximal ideals to maximal ideals, therefore this
element must be in mx. Which means that fi - Qi vanishes at P. I.e.
P,Y . The uniqueness follows from the fact that they're local rings, and also
note that they are given by all the elements that are 0 on P (respectively, Q).
Now taking inspiration from example 1.4.4, note that the regular functions
yi - Qi "determine" the point Q. Indeed they are 0 on Q, so yi - Qi ∈ my.
Now where does ψ-1 send < Y,yi - Qi > to? By (2) and basic k algebra
morphism properties, it gets send to < Ui,fi - Qi >. But since ψ-1 is an
isomorphism, it maps maximal ideals to maximal ideals, therefore this
element must be in mx. Which means that fi - Qi vanishes at P. I.e.
| fi(P) = Qi |
Looking back at the definition of ϕ, it's now clear that ϕ maps P to Q.
PS: Koshka featured leafblowers in a past article, and actually has a rational argument against them that isn't just Bon Jovi lyrics.