I.3.6
4/22/2021
Let's follow the hint. For now let's just assume that
 (X) ≃ k[x,y]. Then if X
were isomorphic to an affine variety Y , then we'd have that
(X) ≃ k[x,y]. Then if X
were isomorphic to an affine variety Y , then we'd have that
 (Y ) ≃
(Y ) ≃
 (X) (see
Lemma 1, here. Hence
(X) (see
Lemma 1, here. Hence
 (Y ) ≃ k[x,y], which means that we must have that
Y ≃ A2 (corollary 3.7). Hence, X ≃ A2. Let's call this isomorphism ϕ:
(Y ) ≃ k[x,y], which means that we must have that
Y ≃ A2 (corollary 3.7). Hence, X ≃ A2. Let's call this isomorphism ϕ:
| ϕ : A2 | → A2 - 0 | ||
Now, the question being begged is if ϕ maps A2 to A2 - 0, where is the origin being mapped to? It has to be mapped somewhere, so let's suppose that ϕ(0, 0) = (R,S)
Now, nothing immediately wrong with that persay. There are isomorphisms of affines that map the origin to nonzero points. Like translations for example, like I've shown before. But WAIT: This map couldn't be a translation. Because then what would (-R,-S) map to? HMMMMMMM.
Something is geometrically wrong with this map. And since this subject is called "algebraic geometry", let's look at what's happening with the induced map of coordinate rings:
| ϕ* : k[x,y] | → k[x,y] | ||
| f |
 f ∘ ϕ f ∘ ϕ |
This map is an isomorphism (again, thanks to Lemma 1 from here). And how is it defined? Well, figuring out how a k-algebra morphism means figuring out where x and y go. Let's start with x.
| x |
 ϕ * (x) ϕ * (x) | ||
| = x ∘ ϕ | |||
| ∈ k[x,y] |
Errr... okay.... Let's try plugging in the special point (0, 0), in which case we get that
| (x ∘ ϕ)(0, 0) | = x(ϕ(0, 0)) | ||
| = x(R,S) | |||
| = R |
Ah, so ϕ * (x) has to be a polynomial that evaluates to R on (0, 0). Which means that it must be a polynomial with a constant term of R:
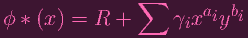 | (1) |
Okay, that thing on the right is kind of complicated. But I believe! I believe that
it's simpler than that. Remember: I had a strong suspicion that this map would
end up representing a translation. could the right hand side, possibly, be simply
x + R?
Well: ϕ* is an isomorphism. Okay. And the fact that ϕ maps (0, 0) to (R,S) is
equivalent to saying that ϕ* maps (x,y) to (x - R,y - S). In particular, it
has to map the generators of the former ideal, x,y to generators of the latter
ideal.
NOW: are the generators of the latter ideal necessarily x - R and y - S? Not
necessarily. But it's pretty clear to see that they have to be at least
linear. So I can write (1) as
| = |
| ϕ * (y) | = S + cx + dy |
OKAY: sooooooo this isn't quite a translation..... BUT, this does tell us that ϕ must look like this:
| (x,y) |
 (R + ax + by,S + cx + dy) (R + ax + by,S + cx + dy) |
And remember: The contradiction I'm looking for is to produce a 0 in the image. Is that possible? Well, I would like.
| ax + by | = -R | ||
| cx + dy | = -S |
BUAHAHAHAHAHA. A system of linear equations. And it's clear to see that it must have full rank (remember we need to generate the maximal ideal (x - R,y - S), and thus has a solution.
SO WE'RE DONE....
Dick: Welcome to Dick & Cock United, where we bring you the
highest quality Dick & Cock goods. I'm Dick
Cock: And I'm Cock.
Dick: And together, of course, we're Dick & Cock.
Cock: Hey Dick.
Dick: What's up, Cock?
Cock: Let's play a game. When I say Dick, you say Cock. Got it? I'll start:
Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Dick: Cock.
Cock: Dick.
Cock: Good stuff, Dick. Gimme a high five.
*Clap*
Dick: Down low!
*Slap*
Dick: Too slow.
Cock: Too small.
 |
Let's call this f. And let's write an analogous polynomial for ϕ * (y)
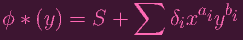 |
Let's call this g. So I can't necessarily claim that f and g are linear (thus
screwing up the "translation" dream). In fact, this is sort of the best I can do
unless I want to use the advanced "automorphism theorem of k[x,y]" linked
above. Fine then I'll have to do with using that as my base map. If that's what
ϕ* is, then ϕ is given by
| (x,y) |
 (R + ∑
γixaiybi,S + ∑
δixaiybi) (R + ∑
γixaiybi,S + ∑
δixaiybi) | ||
| = (f(x,y),g(x,y)) |
Now, why did I want translation or linearity in the first place? I wanted to produce (0, 0) in the image, to yield a contradiction. Indeed, I would like to find a point (x,y) that is zero on both polynomials. I.e. I want Z(f) ∩ Z(g) to be nonempty. Here's the thing. we know that ϕ* maps x
 f and y
f and y
 g. So ϕ must
map (Z(x) ∩ Z(y)) to Z(f) ∩ Z(g). But the former set is nonempty (it
contains (0, 0)), so since ϕ is an isomorphism, the latter set must be nonempty
too.
g. So ϕ must
map (Z(x) ∩ Z(y)) to Z(f) ∩ Z(g). But the former set is nonempty (it
contains (0, 0)), so since ϕ is an isomorphism, the latter set must be nonempty
too. So there you fucking go. FUCKING DONE.
actually, we still need to show that
 (X) ≃ k[x,y].... Fuck.
(X) ≃ k[x,y].... Fuck. Alright. Fine. So
 (X) = S-1k[x,y] where S = {f|f≠0 on X}. Now
let's suppose that f ∈ S. If f is reducible, then it can be factored into
f = g ⋅ h where both g and h must be in S. So let's assume without
loss of generality that f is irreducible. Then f must be nonzero on all of
A2, possibly excluding the origin. Well, if it has no zeros at all, then it
would have to be a constant function (f ∈ k). What if it was 0 at the
origin, and only the origin? Then f(x, 1) would have to be a constant
polynomial (otherwise f(x, 1) would have zeros. Say it had a zero at a. Then
(a, 1) would be a zero of f, contradicting nonzeroness outside the origin).
Actually, this would apply for any f(x,b) where b ∈ k. And I'm PRETTY
SURE that this means that f has no x terms. I know we JUST saw the
consequences of trusting my "pretty sure"ness, but.... I've already spent way too
much time on this. Exercise left to you, dear reader, lol (I'll hoist a hint
for you: plug in 1 and then a large value a >> 1 for y and see what
happens to the like degree x terms in either case.). If you apply this same
"reasoning" to show that f has no y terms either, that means that f ∈ k yet
again. Hence, S = k. Which means that S-1k[x,y] = k[x,y]. DONE.
(X) = S-1k[x,y] where S = {f|f≠0 on X}. Now
let's suppose that f ∈ S. If f is reducible, then it can be factored into
f = g ⋅ h where both g and h must be in S. So let's assume without
loss of generality that f is irreducible. Then f must be nonzero on all of
A2, possibly excluding the origin. Well, if it has no zeros at all, then it
would have to be a constant function (f ∈ k). What if it was 0 at the
origin, and only the origin? Then f(x, 1) would have to be a constant
polynomial (otherwise f(x, 1) would have zeros. Say it had a zero at a. Then
(a, 1) would be a zero of f, contradicting nonzeroness outside the origin).
Actually, this would apply for any f(x,b) where b ∈ k. And I'm PRETTY
SURE that this means that f has no x terms. I know we JUST saw the
consequences of trusting my "pretty sure"ness, but.... I've already spent way too
much time on this. Exercise left to you, dear reader, lol (I'll hoist a hint
for you: plug in 1 and then a large value a >> 1 for y and see what
happens to the like degree x terms in either case.). If you apply this same
"reasoning" to show that f has no y terms either, that means that f ∈ k yet
again. Hence, S = k. Which means that S-1k[x,y] = k[x,y]. DONE.