I.3.2
4/15/2021

"Umm, teacher, when am I going to use the Frobenius morphism in real life?" Ummm, you're not.
You came here to waste your time, not become a better person. You're not going to go out in the
park and see a couple feeding each other icecream and be like, "Ohhh. That's just like the Frobenius
morphism!". If you can think of a situation where the Frobenius morphism saves someone's life, let me know.

Yea, I don't know why I'm here either. I could spend all this free time on self-improvement, attending to
some urgent life things, and finally getting myself together and pulling myself out of the impending
doom that is coming in at many angles towards my near future. BUT remember, reader, as I've said
before: The purpose of this blog is not to get better, but to get worse. So here we are. At least there's a
little "anti-lesson" to be had at the end of this exercise. First we have to handle part (a), though.
PART (a):
Let's start by showing that ϕ is bijective onto Z(y2 - x3).
Given (X,Y ) ∈ Z(y2 - x3), we know that
| X3 - Y 2 | = 0 |
Now, let T,-T be the square roots of X (since we're in an algebraically closed field), so that
| (T2)3 - Y 2 | = 0 | ||
 (T3)2 - Y 2 (T3)2 - Y 2 | = 0 | ||
 (T3 - Y )(T3 + Y ) (T3 - Y )(T3 + Y ) | = 0 |
so that Y = T3 or Y = -T3 = (-T)3. In the former case, let t = T, and in the latter case let t = -T. Then clearly ϕ(t) = (X,Y ). Hence, ϕ is surjective.
So is ϕ injective? Let's see:
| ϕ(t1) | = ϕ(t2) | ||
 (t12,t13) (t12,t13) | = (t22,t23) | ||
 t12 = t22 t12 = t22 | and t13 = t23 | ||
 t1t22 t1t22 | = t23 | ||
 t1t22 - t23 t1t22 - t23 | = 0 | ||
 t22(t1 - t2) t22(t1 - t2) | = 0 |
Great! So ϕ is bijective onto Z(y2 - x3). Now we have to show that it is a homeomorphism.
Let f(x,y) ∈ k[x,y] so Z(f) is a closed set in A2. Then
| T | ∈ ϕ-1(Z(f)) | ||
| ⇐⇒ϕ(T) | ∈ Z(f) | ||
| ⇐⇒f(ϕ(T)) | = 0 | ||
| ⇐⇒f(T,T2) | = 0 |
Hence, letting g(t) = f(t,t2) ∈ k[t], we have that Z(g) = ϕ-1(Z(f)). So ϕ is indeed continuous. IMPORTANT: Note how in this direction, given f in the A2 side, there is an easy way to get a corresponding polynomial g on the A1 side. But what happens when we try the other direction? We need to show that ϕ is a closed map to prove that it's a homeomorphism. But if you give me an element f ∈ k[t], what is ϕ(Z(f))? What polynomial will I get for the A2 side?
I struggled trying to construct one for a good hour or so, and then I realized: wait, if there were a way to get a nice, single polynomial from f, that would actually be a problem: that would indicate that there's an isomorphism of coordinate rings, which would imply that ϕ is an isomorphism, which we know according to the exercise can't be true. Z(f) isn't gonna map to some simple Z(g), it's gonna map to Z(somethingmorecomplicated). But still: what would that be?
Then I realized, oh wait, f comes from a single-indeterminate coordinate ring (k[t]): we can fully factor it into linear factors: f = (t - t0)
 (t - tn). But wait.... that just means that Z(f) is a finite set. So ϕ(Z(f)) is a
finite set, which is trivially closed in A2. (unless f = 0, in which case Z(f) = A1, so ϕ(Z(f)) = A2, since ϕ
is surjective). Oh, right...... I just rederived the fact that A1 has the finite complement topology....
(t - tn). But wait.... that just means that Z(f) is a finite set. So ϕ(Z(f)) is a
finite set, which is trivially closed in A2. (unless f = 0, in which case Z(f) = A1, so ϕ(Z(f)) = A2, since ϕ
is surjective). Oh, right...... I just rederived the fact that A1 has the finite complement topology....

YEP. Well, ϕ is a homeomorphism. Good. One consequence of this, by the way, is that Z(y2 - x3) is irreducible (since A1 is), so it's actually a variety, with coordinate ring k[x,y]∕(y2 - x3). In fact, we can view ϕ : A1 → Z(y2 - x3) as the morphism induced by the following map of coordinate rings
| ψ : k[x,y]∕(x3 - y2) | → k[t] | ||
| x |
 t2 t2 | ||
| y |
 t3 t3 |
So ϕ is therefore a bicontinuous morphism. Finally, since we're talking about affine varieties, the map of coordinate rings tells all: This induced map is clearly not a k-alg isomorphism (since, e.g. ψ is not surjective: it doesn't reach t), hence ϕ is not an isomorphism either. DONE.
PART (b):

Here's the Frobenius morphism! Proof is basically identical to (a), so I'll skip most of it. The most difficult part is showing that ϕ is injective. So let's say we had ϕ(x) = ϕ(y). I.e.
| xp | = yp |
I got stuck here for like an hour or so as well....
Here's the problem: Fixing y, the polynomial xp - yp = 0 could in general have p many solutions for x. One of them is the one we want x = y, but how do we guarantee that will occur? I mean, for that to be the only solution, this polynomial would have to factor into... (x-y)p. Yeah, fucking right. What crazy ass fucking nonsense is that? In your dreams, motherfucke–oh, right.
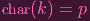 |
THERE U GO, my _______ vision goggle wearers. Do not work hard to make your dreams come true. Work hard to set up a context exotic enough that
they have to come true.