I.2.11a
2/18/2021
Warm, soft reddish flesh, pierced by a primsatically blue icicle.  LINEAR. FUCKING. ALGEBRAAAAAAAAAAA.
LINEAR. FUCKING. ALGEBRAAAAAAAAAAA.
"Pfft, this is easy," says the fancy shmancy rank and determinant afficianado. Listen: I suck assdickshitballs at
linear algebra. It just doesn't come to me. "Bro, check out this neural network I trained using PCA."
Ummmmmmmmmm, I don't care about data, I care about the soul. Which is why I'm doing.... algebraic...
geometry?
And thus we begin! If you're afraid of linear algebra, no worries, just hold my penis vector hand. I'll even figure out
how to draw matrices in Latex. Just for you.
Actually, the first direction, (i)
 (ii) doesn't require any linear algebra at all. Given a variety Y where I(Y ) is
generated by s linear polynomials, say, f0,…,fs-1 (you can tell that I am 0-based indexing for future convenience
lmao),
(ii) doesn't require any linear algebra at all. Given a variety Y where I(Y ) is
generated by s linear polynomials, say, f0,…,fs-1 (you can tell that I am 0-based indexing for future convenience
lmao),
| I(Y ) | = (f0,…,fs-1) | |||||
 Z(I(Y ) Z(I(Y ) | = Z(f0,…,fs-1) | |||||
 Y Y | = Z(f0,…,fs-1) | (Y is a variety, so it's closed) | ||||
 Y Y | = Z(f0) ∩
 ∩ Z(fs-1) ∩ Z(fs-1) |
Which is (ii). So (i)
 (ii) is done.
(ii) is done.Now, it is very tempting to make all those
 s into ⇐⇒s. In fact, that's what I did at first, and realized while
trying to work through (b) (which I have not finished), that it's a little more complicated. Let's try going backwards
through the proof, starting from (ii):
s into ⇐⇒s. In fact, that's what I did at first, and realized while
trying to work through (b) (which I have not finished), that it's a little more complicated. Let's try going backwards
through the proof, starting from (ii):| Y | = Z(f0) ∩
 ∩ Z(fs-1) ∩ Z(fs-1) | ||
 Y Y | = Z(f0,…,fs-1) | ||
 I(Y ) I(Y ) | = I(Z(f0,…,fs-1)) | ||
 I(Y ) I(Y ) | =
 |
Yep! It's another fucking radical in the way. Jesus. You can make a drinking game out of all the times on this blog we need to get rid of a pesky fucking radical (also, do you note that I'm correctly calling it radical instead of "square root" now?)
This is where I got stuck for at least an hour. Then I looked online to see if the ideal generated by linear polynomials was in fact prime (or at least radical). Found out that it was, because of what was apparently linear algebra reasons. Linear algebra? Why is linear algebra releva–ohhhh.... linear polynomials. FUCKING DUH. Yes, It took me hours to realize that this problem was even related to linear algebra in the first place.
Well, the explanations online, at least told me linear algebra was related, but since I'm bad at linear algebra, none of the explanations made sense to me, so I was left to do this on my own. Indeed, I was reunited, as I commonly am, with the irony of not being able to get help on something precisely because I'm bad at it.
So, reader, hold my hand through this. We'll get by. There's an "aha" moment: It arrives as soon as you shake off the fear of having to use double subscripts and write out the polynomials in explicit form. Where ai,j are scalars (i.e. ai,j ∈ k), we can write:
| f0 | = a0,0x0 + a0,1x1 +
 + a0,nxn + a0,nxn | ||
| f1 | = a1,0x0 + a1,1x1 +
 + a1,nxn + a1,nxn | ||
 | |||
| fs-1 | = as-1,0x0 + as-1,0 +
 + as-1,nxn + as-1,nxn |
Errrr.... I'm starting to regret that 0-based indexing. TOO LATE.
The "aha" moment is when you look at that and think "oh, and we're setting all of these equal to 0 (since, as usual, we're finding the zeros of these polynomials), so it's just system of linear equations" (and yes, you think "oh" instead of "aha" because obviously noone actually fucking thinks "aha" in their head).
In fact, let's make the obligatory (s × n + 1) matrix of coefficients:
 | (1) |
(heh, don't worry. I used regex search and replace to avoid killing my hands. However, I shall proceed to kill my
hands for the next equation).
Great! Now let's RREF it. You know... Cause... that's just what you do in linear algebra.... Okay, well, the
reason is that the ideal generated by the RREFd polynomials shouldn't be any different than the
ideal generated by the non-RREFd polynomials, because you can get to RREF by the "elementary
row operations" of Gauss-Jordan Elimination (adding and subtracting elements, and multiplying by
nonzero scalars), which are all operations that can be done and undone in an ideal (the operations
are closed under an ideal, and you can recover the original generators from them by "reversing" the
operations).
Oh, also, if the fis (the row vectors) are linearly dependent, that means we have extraneous generators. Get rid
of some until they become linearly independent (so we get a "minimal" generating set. HMMMM...
sounds similar to part (b)). Hence when we perform RREF we won't get any 0 rows. Also this means
that we can assume that s ≤ n + 1 (otherwise they wouldn't be linearly independent: k[x0,…,xn]
is an n + 1 dimensional vector space over k), i.e. s - 1 ≤ n. Also, we can reorder the variables
without loss of generality, so I'll assume that all the pivot columns come first (I'm grouping all the free
variables so they come last). PHEW. OKAY. So with all that if we RREF we'll get something like
this:
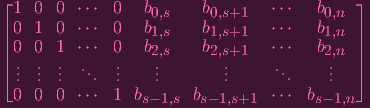 | (2) |
HOLY FUCK I actually used diagonal ellipses *pats self on the back* (with my free hand. My other hand is of
course holding yours).
Might have actually been easier to just use the submatrix notation and use like "Is" and "B" or something like
that.... but anyway this makes it more clear. Remember, we can assume without loss of generality that the
coefficients of f0 are the given by the first row, f1 by the second row, etc. (we basically replaced the original
generators with nicer ones). To make this bitch easier to look at, I'll swallow up those b motherfuckers with some
notation:
| A0 | = b0,sxs + b0,s+1xs+1 +
 + b0,nxn + b0,nxn | ||
| A1 | = b1,sxs + b1,s+1xs+1 +
 + b1,nxn + b1,nxn | ||
 | |||
| As-1 | = bs-1,sxs + bs-1,s+1xs+1 +
 + bs-1,nxn + bs-1,nxn | ||
| x0 | = -A0 | ||
| x1 | = -A1 | ||
 | |||
| xs-1 | = -As-1 |
"WTF are we doing?" Yes, it feels like we're getting kind of off track here. "What does this have to do with getting rid of the square root?" I think you mean "radical" reader. But yes, good question. What does this have to do with showing that J = (f0,…,fs-1) is prime? Well, what we're really saying is that, given these relationships in J, x0,…,xs-1 are kind of "extraneous", since we can just write them in terms of the other (free) variables. I.e. what I'm saying is, it appears that k[x0,…,xn]∕J
 k[x
s,…,xn]. If this is true, then J has to be prime because the
right hand side is an integral domain. So if we show that equality, we're all good. And of course one way to do this is
via the good old first isomorphism theorem . I.e. I'll create a surjective morphism whose kernel is J.
Let
k[x
s,…,xn]. If this is true, then J has to be prime because the
right hand side is an integral domain. So if we show that equality, we're all good. And of course one way to do this is
via the good old first isomorphism theorem . I.e. I'll create a surjective morphism whose kernel is J.
Let
![ϕ : k[x0,...,xs- 1] → k[xs,...,xn ]](Ip2p11a24x.png) | (3) |
given by xi
 xi if i ≥ s (if it's a free variable), and xi
xi if i ≥ s (if it's a free variable), and xi
 -Ai if i < s. Oh, and a
-Ai if i < s. Oh, and a
 a if a is a scalar. Starting
to sound familiar? Yes. It's basically the same thing you do in the very first exercise (and 1.2). OH GOD MY
WRITING BACK THEN WAS SO CRINGE HOLY FUCK DON'T CLICK (well my writing even like 1 post before
this one is pretty cringe but cringe gains interest over time).
a if a is a scalar. Starting
to sound familiar? Yes. It's basically the same thing you do in the very first exercise (and 1.2). OH GOD MY
WRITING BACK THEN WAS SO CRINGE HOLY FUCK DON'T CLICK (well my writing even like 1 post before
this one is pretty cringe but cringe gains interest over time).
I'll at least partly restate the process here (since I am now better at writing this out and also BOTH OF THOSE
FUCKING OLD POSTS HAVE TYPOS IN THIS PART LOL), by construction, J ⊂ ker ϕ and
for the reverse inclusion, given some g ∈ ker ϕ we're going to divide out the fis using
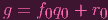 | (4) |
where q0 is some quotient and r0 is a remainder with lesser degree over x0 then f0. I.e. r0 has no x0 terms, so it can be seen as a polynomial in just k[x1,…,xn] (we got rid of the x0). Now we divide r0 by f1, etc. etc. and you get
 | (5) |
where rs-1 ∈ k[xs,…,xn]. Taking ϕ of both sides of the above equation clearly gives you (using the fact that
g,f0,f1,…,fs-1 ∈ ker ϕ)
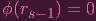 | (6) |
Write rs-1 = ∑
i=snaixi so that
| ϕ(rs-1) | = 0 | ||
 ϕ(∑
i=snaixi) ϕ(∑
i=snaixi) | = 0 | ||
 ∑
i=snϕ(aixi) ∑
i=snϕ(aixi) | = 0 | ||
 ∑
i=snϕ(ai)ϕ(xi) ∑
i=snϕ(ai)ϕ(xi) | = 0 | ||
 ∑
i=snaixi ∑
i=snaixi | = 0 | ||
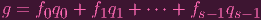 | (7) |
i.e. g ∈ J, so ker ϕ ⊂ J.
HENCE. WE. ARE. DONE. AND. WE. CAN. GET. RID. OF. THE. SQUARE. ROOT. I. MEAN.
"RADICAL".