And with it, comes a cute little picture:

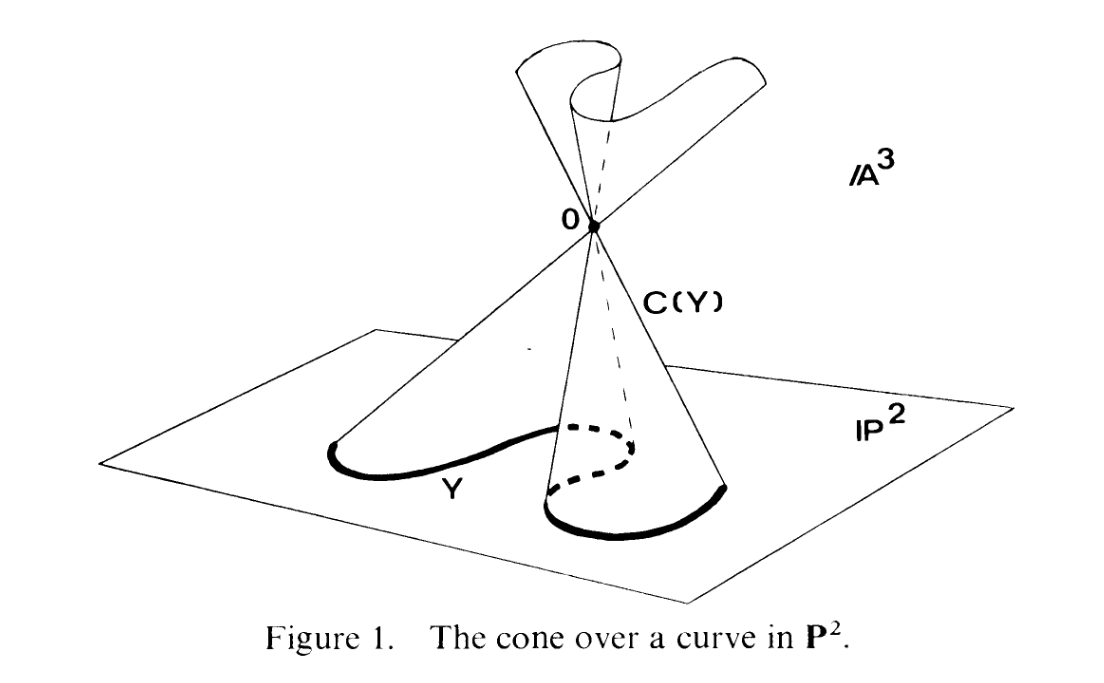
Ooo, fancy. As usual, my visualization skills for projective spaces are lackluster to say the least, but this picture appears to suggest that I can essentially just think of Pⁿ as typical n-dimensional space, with some "infinity points" added in..... sort of..... kind of.... ANYWAY, let's get on with it.

Note that θ is surjective, so

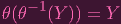(1)

Showing that C(Y )'s ideal is equal to I(Y ) is asking us to show that I(C(Y )) = I(Y ) (where technically the first I is taken in affine space and the latter is taken in projective space, but I won't work that into the notation, cause my skillz have advanced since 2.1)

Consider a homogenous polynomial f. Then...

f	∈ I(C(Y ))
⇐⇒∀P ∈ C(Y )	: f(P) = 0
⇐⇒f(0) = 0 and ∀P ∈ θ-1(Y )	: f(P) = 0
⇐⇒∀P ∈ θ-1(Y )	: f(P) = 0	(f(0) = 0 is automatic since f is homogenous)..... WAIT. ARE YOU SEEING THIS? I FIGURED OUT A WAY TO FIX THE FUCKING "STICKING OUT" ISSUE HOLY PFUCKING SHIT LET ME FUCKING THROW IN A BUNCH OF TEXT AND ABUSE THIS NEWFOUND TECHNIQUE WOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO (...well I need to break the text more elegantly)
⇐⇒∀P ∈ θ-1(Y )	: f(θ(P)) = 0	(again, by homogeneity of f)
⇐⇒∀Q ∈ Y	: f(Q) = 0	(basic set theory: (1))
⇐⇒f	∈ I(Y )

Hence, I(Y ) and I(C(Y )) share all the same homogenous elements (I(Y ) ∩ S^h = I(C(Y )) ∩ S^h). Do they turn out to be the same ideal?

Well, we'll get to that, but let's take a little detour, cause we have enough information to at least show that C(Y ) is algebraic.

Suppose we had P ∈C(Y ), but P 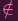C(Y ) The latter expression implies that P 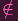θ^-1(Y ). And note that C(Y ) = Z(I(C(Y ))), so the former expression means that P would satisfy:

∀f ∈ I(C(Y ))	: f(P) = 0
∀f ∈ I(C(Y )) ∩ Sh	: f(P) = 0
∀f ∈ I(Y ) ∩ Sh	: f(P) = 0
∀f ∈ I(Y ) ∩ Sh	: f(θ(P)) = 0	(f is homogenous)
θ(P)	∈ Z(I(Y ))	(Definition of Z in projective space)
θ(P)	∈ Y	(Y is algebraic)
P	∈ θ-1(Y )

and that last expression is a contradiction. Hence, this P cannot exist, and we must have C(Y ) = C(Y ). So C(Y ) is indeed algebraic.

Okie dokie. Now we can show that I(C(Y )) = I(Y ), and for the first inclusion we'll use the fact that we've already shown that they share the same homogenous elements.

It's clear that I(Y ) ⊂ I(C(Y )), since any nonhomogenous element in the former is generated by homogenous elements, and since the latter contains the same homogenous elements, we can generate that nonhomogenous element in the latter as well (this disaster of a sentence is what happens when you try explain math through English instead of notation)

So now for the reverse inclusion. Consider f ∈ I(C(Y )) that is nonhomogenous (well the argument still applies for homogenous lol). And suppose deg f = d. Then group the i degree monomials of f together as f_i, and write f as a sum (i.e. we're writing f as a sum of its homogenous components):

(2)

(Note that we can exclude i = 0 because 0 ∈ C(Y ), so f can't have any nonzero zero-degree terms)
Note: f ∈ I(C(Y )) ∀P ∈ θ^-1(Y ) : f(P) = 0. Consider any random P ∈ θ^-1(Y ), so that f(P) = 0. Note that also cP ∈ θ^-1(Y ) for any scalar c ∈ k, which means we'd have to have f(cP) = 0 So....

∑ i=1dfi(cP)	= 0
fd(cP) + fd-1(cP) + + f1(cP)	= 0
cdfd(P) + cd-1fd-1(cP) + + cf1(cP)	= 0
- (cd-1fd-1(cP) + + cf1(cP))	= cdfd(P)

Now if f_d(P) is nonzero, then the left hand side can be thought of a d degree polynomial in c, P(c), and the right hand side can be thought of an at most d - 1 degree polynomial Q(c). But a d-degree polynomial can't equal a ≤ d - 1 degree polynomial (not over an algebraically closed field, at least... I think), so we have to have f_d(P) = 0. Now, repeat this process for each degree and you get

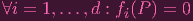(3)

Now since P was arbitrary, this applies for any P ∈ θ^-1(Y ). But with each f_i being homogenous, this means that

(4)

which means that by (1) f₁,…,f_d ∈ I(Y ). But I(Y ) is an ideal, so f = f₁ + + f_d ∈ I(Y ).

Since f was arbitrary, I(C(Y )) ⊂ I(Y )

Dun. Whew. uhhhh, here's where I would spend some time analyzing the figure and talking about the visual explanation but i'm too tired rn CYA IN PART B.