I.1.7c
12/24/20

Merry fuck you eve. This one is quick
Let Y be a subspace of X, where X is Noetherian. We want to show that Y is Noetherian.
Suppose we have a chain
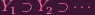 | (1) |
of closed subsets of Y
Note, by the subspace topology, for each i = 1,2,…:
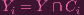 | (2) |
for some Ci closed in X.
For each i, let
 | (3) |
and note that each Di is closed in X.
Then the chain
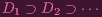 | (4) |
stabilizes since X is Noetherian. So for some n,
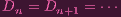 | (5) |
Note: ∀k < i, Y k ⊃ Y i, so
| Y i | = Y i ∩ Y i-1 ∩ ∩ Y 1 ∩ Y 1 | (6) | ||
= (Y ∩ Ci) ∩ (Y ∩ Ci-1) ∩ ∩ (Y ∩ C1) ∩ (Y ∩ C1) | (By (2)) | (7) | ||
= Y ∩ Ci ∩ Ci-1 ∩ ∩ C1 ∩ C1 | (8) | |||
| = Y ∩ Di | (9) |
But intersecting Y with (5) yields
Y ∩ Dn = Y ∩ Dn+1 =  | (10) | |
 Y n = Y n+1 = Y n = Y n+1 =  | (using (9)) | (11) |
| (12) |
So we're done. WELP, THE EQUATION NUMBERS ARE ALL FORMATTED FUCKED UP, BUT FUCK IT.