I.1.1b
11/24/2020
Here’s today’s exercise:

I’m aware that my solution to yesterday’s exercise had issues. I am not going back and editing them up because this
blog isn’t meant to be a solution guide. It’s meant to be an exposure of my incomptence. But I will add an ”errata”
section at the end of THIS post to cover them errorz.
Part b was not any easier than part a. But let’s begin.
A(Z) = k[x,y]∕(I(Z(xy - 1)) = k[x,y]∕(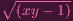 ).
).
And of course, I’d like to get rid of that square root, so my first instinct is to show xy-1 is irreducible
(prime), therefore radical. But this time I was smart enough to say, ”Hey, let me not spell out the
half the alphabet this time.” So you know what I did? I spelled out half the alphabet. WAIT, I can
explain.
This time I have to show that A(Z)≠k[z]. Well, showing two things are NOT isomorphic is harder than showing that
they are. the easiest way is to find a property that is satisfied by one but not the other. Now, thinking back to that
integral domain trick from earlier. I thought, hey, maybe A(Z) is not an integral domain whilek[z] is. Well A(Z) not being
an integral domain means that  isn’t prime, i.e. it’s reducible. And if it’s reducible that means Z(xy - 1)
is, which makes sense because if you graph y = 1∕x you see two separate components, so it’s reducible... right?
isn’t prime, i.e. it’s reducible. And if it’s reducible that means Z(xy - 1)
is, which makes sense because if you graph y = 1∕x you see two separate components, so it’s reducible... right?
So I actually changed my mind: I WANT f=xy-1 to be reducible. Okay, can you think of any ”reduction” of this f off
the top of your head? I couldn’t. I need two nonunits g,h such that gh = f. And since the max degree of x and y on f
are both 1, I know that g and h must be of the form
g = axy + bx + cy + d
h = ixy + jx + ky + l
So I spelled out half the alphabet again...
And guess what I found? There is no assignment of a-l that makes it work. So xy-1 is irreducible, and now I don’t
fucking know what the visual intuition for irreducibility is because Z(xy-1) looks fucking reducible on the
graph.
Fuck intuition then.
Well, I guess xy-1 is irreducible. Great. At least now  = (xy - 1)
= (xy - 1)
So I have to show that
k[x,y]/(xy-1) != k[z]
Just call the left side R for now. So I need to show R != k[z]. I need to find an isomorphism-invariant property that
holds for one but not the other.
Now listen folks: I’m not a math student. My degree was in STEM, but I only know what I know about abstract
algebra and shit like that by half-assedly reading about them. So I don’t know what the correct technique here is.
What did I try? Well, k[z] is a principal ideal and k[x,y] isn’t. I remember hearing that (x,y) is a maximal ideal in
k[x,y] (actually, it’s example 1.4.4 in the book, which took me like 30 minutes to verify and I don’t remember how
the fuck it works anymore, but I guess that’s how it is–HOWEVER it doesn’t show that (x,y) is NOT principal, so
it’s not helpful after all), so maybe quotienting it with (xy-1) doesn’t change that fact. So I tried to show that (x,y)
in R is not principal (going off the last parenthetical, I haven’t even proven that it was nonprincipal in
k[x,y], so I should have known what a treat I would be in for), and let’s just say it didn’t work out. I
spelled out half the alphabet in my attempt again and spent 2 hours in vain, but I won’t divulge
you with the details, as although it would be very funny to look, it would be too long to type out.
Now, reader, you’ll have to excuse me. Excluding the appendices, there are a total of over 40 sections in this
book. I added up the exact number 5 seconds ago but already forgot it. It’s over 40. This section,
I.1.1, has 12 exercises. Realistically, I can only do 1 exercise every 2 days. No, this first exercise had
2 parts, a and b, and it took me 2 days to to EACH. Actually it has a part c too, but it’s starred,
which means its practically invisible to my noob eyes. I’m not even going to read what it says ”out of
curiosity”. ”But OMG, mathematicians are driven by curiosity. Thats like totally the best part of
math. Solving puzzles, exploring, working thru hard problems. it can be frustrating at times, but the
challenge is what makes it fun and its worth it for the discoveries you make.” Shut the fuck up, you
asslicking dickwad. Go suck on part c (c stands for cock) all you want. I’m not even looking at it.
Back to the point: let’s be generous and say 1 exercise every 2 days, and let’s say there are about 10 exercises per a
section. Then each section would take me 2*10=20 days, almost a month. And there are over 40 sections. So in
total, finishing the book would take at least 40*2*10=800 days. That’s OVER 2 FUCKING YEARS. All these
fucking online ”Do EVERY exercise” assholes can suck my tiny noob cock. I’m not falling for your shitty
ass LARP. ”All the exercises” my dick. Even if I only do 5 exercises in each section, this will take
me 40*2*5=400 days in total, over a year. How in the living mother of hell do people work through
these books? I see people saying, ”Oh yea, I just worked through Hatcher this summer. Was pretty
cool.” How is it fucking possible? Really: Like I just did here, I’ve looked into other textbooks, and did
the arithmetic (but not the math, HAHA). It doesn’t seem like there’s enough time to work through
an entire textbook over the summer, even if you only do less than half the exercises in each section.
Either all mathematicians are LARPing or I’m megabad. Well, I guess it’s gotta be the latter, huh?
So how’s a megabadass *gets sneered at* I mean a megabad layman like me supposed to get by? Fine, I’m going to
only do 5 exercises in each section. It will still take at least 400 days, which is too much, but I’ll find a way to shave
off time as I move forward. But finishing the whole book in that amount of time does assume that I do each exercise
in 2 days. So, y’see, when I see the hour hand inching upwards, approaching the horizontal, I find myself in a tough
spot.
Basically, what I’m trying to say is that I looked up a hint in order to finish this exercise. And in the future I will
probably look up the full solution for exercises I’m really stumped on (but I will always be honest with you, dear
reader, when I do). That’s life for the the megalayass.
Some guy online says to find units that add to a unit in R, since that can’t happen in k[x,y] Well, good thing I
looked this shit up, because I never would have thought of that as the isomorphism invariant property to use here.
Though I guess from now on I’ll consider that for quotient rings.
Well, I have to verify for myself that it is in fact an iso-inv prop, so I’m going to do that. I’ll prove the following
lemma:
Suppose A B and in A, units add only to units. Then in B units add only to units.
B and in A, units add only to units. Then in B units add only to units.
Okay. Since A B there is an isomorphism ϕ : B → A. Suppose u,v are units in B. Then
u + v = ϕ-1(ϕ(u + v)) = ϕ-1(ϕ(u) + ϕ(v)) = ϕ-1(a + b)
B there is an isomorphism ϕ : B → A. Suppose u,v are units in B. Then
u + v = ϕ-1(ϕ(u + v)) = ϕ-1(ϕ(u) + ϕ(v)) = ϕ-1(a + b)
Now morphisms map units to units so a and b are units, and a+b is a unit by assumption. And again, since
morphisms map units to units, ϕ-1(a + b) is a unit. Done.
So if we find units in R that map to nonunits, then by the contrapositive of the lemma, either k[x] has units that
add to nonunits or k[x] ≇ R. The former is ”obviously” not true, so the latter must be true, which is what we want.
So we need to find units in R that map to nonunits. x and y are units, since xy = 1. But x + y isn’t a unit. How do I
know this? I have no fucking idea. Maybe it’s not. But fuck it, the hour hand is getting erect and I’m getting horny.
We’ll ride with it.
ERRATA ON 1.1a:
For 1.1a, I correctly viewed g as an element of k[x][y], but then I did Euclidean divison as if it were in k[y][x]. So shit
is really fucked there, but if you do it the right way you’ll get the remainder is r(x,y) = r(x) and the argument
generally works from there I think.
I also should have mentioned that we need f to be surjective, and it clearly is.
MISC:
I used tex4ht again to generate this, except I used the make4ht command instead this time. I don't know if it made any difference.
I also need to add "next" and "back" button to these pages sometime (...if this continues)
Fuck, I just realized I spelled "Hartshorne" incorrectly. Now I have to go fix all the file names and crap too. Not tonight though. Fuck that.