1.1a
11/22/2020
Here's the exercise (Harthshorne, Algebraic Geometry. Easy as fuck to pirate):
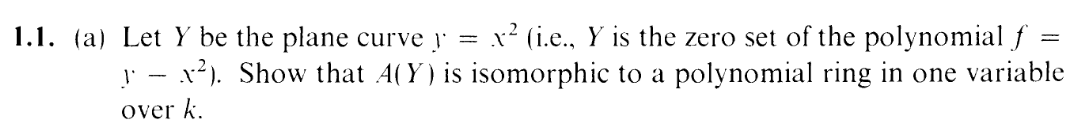
And so we begin. First exercise of the book! Easy, right?
WRONG.
Not for an idiot like me, at least. But let’s get started.
We need to show A(Y ) = k[w].
And in the text he defines A(Y ) = k[x,y]∕I(Y )
So what’s I(Y )?
Well, like he says, Y = Z(f) so
I(Y ) = I(Z(f)) = 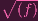 (Nullstellensatz)
(Nullstellensatz)
Oh boy, I sure do hope f is irreducible, cause I know that prime = irreducible in k[x,y] and prime ideals are radical.
So then I’d get 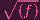 = (f) = (y - x2), which means k[x,y]∕I(Y ) = k[x,y]∕
= (f) = (y - x2), which means k[x,y]∕I(Y ) = k[x,y]∕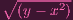 = k[x,y]∕(y - x2)
= k[x,y]∕(y - x2)
So then I’d just have to show that k[x,y]∕(y - x2) = k[w].
so we’d like f to be irreducible. Want to do it the dumbass way, like I did at first? Haha, okay, let’s take a look.
Here’s what I wrote.
f(x,y) = ax2 + bxy + cx + dy + e
g(x,y) = hx2 + ixy + jx + ky + l
and I showed that if fg = y - x2 for nonunits f,g then you get a contradiction (yeah, I at least had the sense to
note that since w’re in an integral domain, I could consider only terms with a degree ≤ 2 in x and
≤ 1 in y in order to multiply to y = x2). Yes. I said, suppose a != 0, made a contradiction. Set a=0.
Suppose b != 0, made a contradiction. Set a,b=0. Suppose c!=0... Etc etc. one by one, till with excruciating bookkeeping, I eliminated a-d and
got left with e, making f a unit. I wiped my forehead, patted myself on the back, smiled, thought,
”Hey, maybe... I do have hope in this world. Maybe it’s time to stop beating myself up, and put my
chin up. Maybe... I actually have a chance in this world. I’m not that bad of a person. I’m actually
an alright person when you think about it. If I put my mind to it, then I can get things done” then
realized it was a waste of fucking time because you automatically get the fucking result at the end
anyway.
When you show k[x,y]∕(y -x2) = k[w], note that k[w] is an integral domain. Right, that means (y -x2) is prime, so
it’s irreducible. So you’re fucking already done once you finish that part and you don’t have to spell out half the
fucking alphabet like I did.
Fine. Less work, right? Let’s show that k[x,y]∕(y - x2) = k[w]. We’re gonna do this by creating a
morphism
f : k[x,y] → k[w]
whose kernel is (y - x2)
”Wait, why did you name it f? You already labelled f as y - x2!” Because I already wrote the damn thing out,
fuckface.
Got it. So let’s start by forcing (y - x2) ⊂ kerf, which is equivalent to y - x2 ∈ kerf. i.e. we want, at least
f(y -x2) = 0. Since f is a morphism, this means we gotta have f(y) -f(x2) = 0 f(y) = f(x2)
f(y) = f(x2) f(y) = [f(x)]2.
f(y) = [f(x)]2.
The most natural assignment satisfying this here would be
f(x) = w
f(y) = w2
f(a) = a (a a constant)
So a ”k-alg morphism”. (BTW, I hesitated a lot here because this choice is ”natural” but also slightly arbitrary. I
realized, wait, theoretically couldn’t there be a ring homomorphism that doesn’t send a to a? Actually
I swear I once saw a ring automorphism of R[x] that didn’t send x to itself or some cray cray shit
like that, but I can’t find it right now. someone let me know if they know what I’m talking
about)
Sooo that determines f, and by construction (y - x2) ⊂ kerf
Now we need kerf ⊂ (y - x2).
Fuck my ass. Confession: I spent at least 4 hours over the course of 2 days trying to prove this. At least. 4. Fucking.
Hours. This is the first exercise in the fucking book. Maybe it’s time to quit.
Well, reader, I confess: looked it up. Shoot me. Yes, I looked it up like a bad student instead of ”asking the teacher”,
because I don’t have a fucking teacher. I saw someone mention ”k[x][y]” and ”Euclidean division” and went from
there.
So yes, consider some g in kerf. (so f(g) = 0) And in particular see g as an elem of (k[x])[y]. I.e. a polynomial in y
where the coefficients are polynomials in x. (I.e., you could express it in "std form" as g = ∑
1ngi(y)xi).
Now perform Euclidean division (where the degree on x determines the degree), with (y - x2) as the
divisor.
g(x,y) = q(x,y) * (y - x2) + r(x,y)
Note that if r(x,y) = 0, we’re done. BTW, what is the degree of r(x,y) as apolynomial in x? well
deg r < deg(y - x2) = 1. So deg r = 0. Yeah, bitch. I don’t have to write ”r(x,y)” I can just write
”r(y)”
sooo, taking f() of both sides, the left hand side is 0 (remember f(g) = 0), and (y -x2) turns into (w2 -w2) = 0. So
you’re left with
0 = r(w)
Okay. Almost there. One more step. Now, some of you folks may find it obvious that r(y) = 0 from here. I had to
think about it. Fuck you. I'm going to prove it explicitly. Note that under f, by definition, the coefficients of r(y) copied onto the coefficients of r(w). r(w) = 0
means that all said coefficients are 0. So r(y) = 0. Mhm, I had to justify that to myself. Mhm, you got a problem
with that?
Annnnnd we’re done. g ⊂ kerf, so kerf = (y - x2).
What a fucking pain. Part b soon, if I can even figure it out. I hate myself I hate myself I hate myself I hate
mys...
By the way, I generated this using tex4ht. All I had to write was "htlatex myfile.tex" and it did everything for me. As you can see it's not... perfect (that summation from earlier looks like Cthlulu), but maybe I'll learn how to use it as this goes on. If it does...